Ao final do século XV a álgebra pouco evoluíra em relação ao conhecimento que egípcios e babilônios tinham sobre o assunto 1800 anos antes de Cristo. O mais antigo livro impresso sobre aritmética e álgebra, a Summa (1494), do frade italiano Luca Pacioli (1445-1515), dá bem uma ideia desse fato, pois no que se refere à álgebra essa obra se limita à resolução de equações de primeiro e segundo graus e assim mesmo (como era usual na época) por meio de regras verbais aplicadas a casos numéricos. E Pacioli terminava seu livro afirmando ser a solução da cúbica $x^3+mx=n$ (usando a notação moderna, $m>0$ e $n>0$ tão possível quanto a quadratura do círculo.
Mas esta previsão logo iria ser desmentida. Aproximadamente na virada do século XV para XVI, Scipione del Ferro (1465-1526), professor da Universidade de Bolonha, conseguiu resolver esse tipo de equação. Ora, como a substituição:
$$x = y-\left(\frac{a}{3}\right)
$$
transforma:
$$x^3+ax^2+bx+c=0
$$
em uma equação do tipo:
$$y^3+py+q=0
$$
então o segredo da resolução das equações cúbicas esta praticamente desvendado.
Scipione contudo não publicou seu método. Apenas o segredou, tempos depois, a Antonio Maria Fiore e seu genro (e futuro sucessor em Bolonha) Annibale della Nave. Diga-se de passagem que era comum na época guardar segredo de resultados científicos obtidos a fim de usá-los como trunfos em porfias intelectuais que com certa frequência ocorriam e que acabavam servindo de avaliação científica dos participantes.
Nesta altura entra em cena Niccolo Fontana (1499?-1557), natural de Brescia, na Itália. Quando em 1512 sua cidade natal foi invadida pelos franceses, mesmo estando refugiado na catedral local com outros habitantes, foi seriamente ferido, tendo inclusive seu palato perfurado por um golpe de sabre. Sobreviveu a duras penas, tanto mais que era órfão de pai e muito pobre, mas contraiu uma gagueira que o acompanhou pelo resto da vida - daí o apelido consequente de Tartaglia (Tartamudo: aquele que possui imperfeições na fala). Felizmente sua brilhante inteligência não foi afetada e ainda bem jovem, como autodidata, tornou-se um respeitável professor de matemática.
Por volta de 1530 acabou vazando a notícia de que Tartaglia saberia resolver uma equação cúbica incompleta da forma:
$$x^3 + px + q =0
$$
Achando tratar-se de bravata, quando soube disso, Fiore desafiou Tartaglia para uma disputa envolvendo cúbicas. Realizada em 1535, com cada um propondo 30 questões para o outro, Tartaglia ganhou de 30 a zero, o que fez sua fama crescer enormemente.
Apesar da intenção de manter segredo de seus métodos sobre o assunto, Tartaglia acabou por revelá-los (sob promessa de sigilo) ao matemático, médico, astrônomo e astrólogo Girolamo Cardano (1501-1576). Cardano, do ponto de vista intelectual era inquestionavelmente brilhante, quanto ao caráter era no mínimo uma figura controvertida. E qual não foi surpresa de Tartaglia quando, em 1545, ao sair a primeira edição do importante livro Ars magna (Arte maior), de autoria de Cardano, lá estavam seus métodos, embora com referência de agradecimento a ele, o que gerou uma polêmica infrutífera de mais de um ano entre ambos.
O fato é que a longa e retórica solução de $x^3+px+q=0$, que figura no Ars magna e que em notação atual se traduz por:
$$\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}
$$
hoje é conhecida como fórmula de Cardano-Tartaglia.
O Ars magna incluía outra notável descoberta, devida a Ludovico Ferrari (1522-1565), discípulo de Cardano: um método para reduzir equações do quarto grau a equações cúbicas. Neste ponto, praticamente, a álgebra iria ficar por quase dois séculos e meio.
Resolvendo uma equação cúbica pelo método de Cardano-Tartaglia
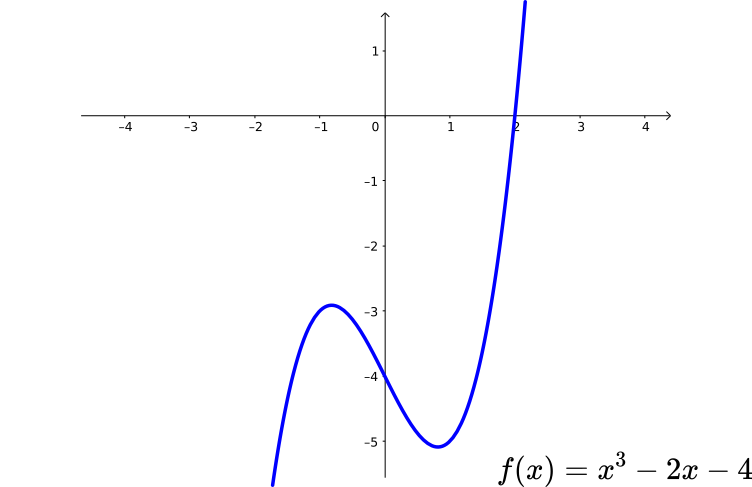
Dada a cúbica $f(x)=x^3-2x-4$, vamos aplicar a fórmula dada acima para encontrar pelo menos uma raiz real.
O gráfico desta função pode ser visto abaixo. Podemos perceber que a curva corta apenas uma vez o eixo dos $x$. Isso quer dizer que a cúbica possui apenas uma raiz real.
Esta parte do artigo tem melhor visualização em telas horizontais. Se necessário, gire a tela de seu dispositivo para ver as equações completas.
Seja a equação $x^3-2x-4=0$. Fazemos $p=-2$ e $q=-4$. Assim:
$$
x =\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\\
\ \\
x = \sqrt[3]{-\frac{(-4)}{2}+\sqrt{\frac{(-4)^2}{4}+\frac{(-2)^3}{27}}}+ \\ +\sqrt[3]{-\frac{(-4)}{2}-\sqrt{\frac{(-4)^2}{4}+\frac{(-2)^3}{27}}}\\
\ \\
x = \sqrt[3]{2+\sqrt{4-\frac{8}{27}}}+\sqrt[3]{2-\sqrt{4-\frac{8}{27}}}\\
\ \\
x = \sqrt[3]{2+\sqrt{\frac{100}{27}}}+\sqrt[3]{2-\sqrt{\frac{100}{27}}}\\
\ \\
x = \sqrt[3]{2+\frac{\sqrt{100}}{\sqrt{27}}}+\sqrt[3]{2-\frac{\sqrt{100}}{\sqrt{27}}}\\
\ \\
x = \sqrt[3]{2+\frac{10}{3\sqrt{3}}}+\sqrt[3]{2-\frac{10}{3\sqrt{3}}}\\
$$
x =\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\\
\ \\
x = \sqrt[3]{-\frac{(-4)}{2}+\sqrt{\frac{(-4)^2}{4}+\frac{(-2)^3}{27}}}+ \\ +\sqrt[3]{-\frac{(-4)}{2}-\sqrt{\frac{(-4)^2}{4}+\frac{(-2)^3}{27}}}\\
\ \\
x = \sqrt[3]{2+\sqrt{4-\frac{8}{27}}}+\sqrt[3]{2-\sqrt{4-\frac{8}{27}}}\\
\ \\
x = \sqrt[3]{2+\sqrt{\frac{100}{27}}}+\sqrt[3]{2-\sqrt{\frac{100}{27}}}\\
\ \\
x = \sqrt[3]{2+\frac{\sqrt{100}}{\sqrt{27}}}+\sqrt[3]{2-\frac{\sqrt{100}}{\sqrt{27}}}\\
\ \\
x = \sqrt[3]{2+\frac{10}{3\sqrt{3}}}+\sqrt[3]{2-\frac{10}{3\sqrt{3}}}\\
$$
Racionalizando o denominador:
$$
x = \sqrt[3]{2+\frac{10}{3\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}}+\sqrt[3]{2-\frac{10}{3\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}}\\
\ \\
x = \sqrt[3]{2+\frac{10\sqrt{3}}{9}}+\sqrt[3]{2-\frac{10\sqrt{3}}{9}}\\
\ \\
x = \sqrt[3]{\frac{18+10\sqrt{3}}{9}}+\sqrt[3]{\frac{18-10\sqrt{3}}{9}}\\
$$
x = \sqrt[3]{2+\frac{10}{3\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}}+\sqrt[3]{2-\frac{10}{3\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}}\\
\ \\
x = \sqrt[3]{2+\frac{10\sqrt{3}}{9}}+\sqrt[3]{2-\frac{10\sqrt{3}}{9}}\\
\ \\
x = \sqrt[3]{\frac{18+10\sqrt{3}}{9}}+\sqrt[3]{\frac{18-10\sqrt{3}}{9}}\\
$$
Fatorando os radicandos:
$$
x = \sqrt[3]{\frac{2\Big(9+5\sqrt{3}\Big)}{9}}+\sqrt[3]{\frac{2\Big(9-5\sqrt{3}\Big)}{9}}\\
\ \\
x = \frac{\sqrt[3]{2\Big(9+5\sqrt{3}\Big)}}{\sqrt[3]{9}} + \frac{\sqrt[3]{2\Big(9-5\sqrt{3}\Big)}}{\sqrt[3]{9}}
$$
x = \sqrt[3]{\frac{2\Big(9+5\sqrt{3}\Big)}{9}}+\sqrt[3]{\frac{2\Big(9-5\sqrt{3}\Big)}{9}}\\
\ \\
x = \frac{\sqrt[3]{2\Big(9+5\sqrt{3}\Big)}}{\sqrt[3]{9}} + \frac{\sqrt[3]{2\Big(9-5\sqrt{3}\Big)}}{\sqrt[3]{9}}
$$
Racionalizando os denominadores:
$$
x = \frac{\sqrt[3]{2\Big(9+5\sqrt{3}\Big)}}{\sqrt[3]{9}}\cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}} + \frac{\sqrt[3]{2\Big(9-5\sqrt{3}\Big)}}{\sqrt[3]{9}}\cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}}\\
\ \\
x =\frac{\sqrt[3]{6\Big(9+5\sqrt{3}\Big)}}{3} + \frac{\sqrt[3]{6\Big(9-5\sqrt{3}\Big)}}{3}
$$
(a+b)^3 = a^3+3a^2b+3ab^2+b^3\\
\ \\
\text{e}\\
\ \\
(a-b)^3 = a^3-3a^2b+3ab^2-b^3
$$
x =\frac{\sqrt[3]{M}}{3} + \frac{\sqrt[3]{N}}{3}
$$
x = \frac{\sqrt[3]{2\Big(9+5\sqrt{3}\Big)}}{\sqrt[3]{9}}\cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}} + \frac{\sqrt[3]{2\Big(9-5\sqrt{3}\Big)}}{\sqrt[3]{9}}\cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}}\\
\ \\
x =\frac{\sqrt[3]{6\Big(9+5\sqrt{3}\Big)}}{3} + \frac{\sqrt[3]{6\Big(9-5\sqrt{3}\Big)}}{3}
$$
Aqui precisaremos fazer uma manipulação algébrica utilizando o produto notável do cubo da soma e cubo da diferença, mas ao contrário. Ou seja já temos nos radicandos dos numeradores a forma expandida e vamos manipulá-los de forma a obter a forma fatorada. Lembrando que:
$$(a+b)^3 = a^3+3a^2b+3ab^2+b^3\\
\ \\
\text{e}\\
\ \\
(a-b)^3 = a^3-3a^2b+3ab^2-b^3
$$
Vamos chamar os radicando de $M$ e $N$ para facilitar a visualização do desenvolvimento:
$$x =\frac{\sqrt[3]{M}}{3} + \frac{\sqrt[3]{N}}{3}
$$
Assim, para o cubo da soma, fazemos:
$$
M = 6\Big(9+5\sqrt{3}\Big)\\
\ \\
M = 54+30\sqrt{3}\\
\ \\
M = 27+27+27\sqrt{3}+3\sqrt{3}\\
\ \\
M = 27+27\sqrt{3}+9\Big(\sqrt{3}\Big)^2+\Big(\sqrt{3}\Big)^3\\
\ \\
M = 3^3+3\cdot 3^2\sqrt{3}+3\cdot 3 \Big(\sqrt{3}\Big)^2 + \Big(\sqrt{3}\Big)^3
$$
M = 6\Big(9+5\sqrt{3}\Big)\\
\ \\
M = 54+30\sqrt{3}\\
\ \\
M = 27+27+27\sqrt{3}+3\sqrt{3}\\
\ \\
M = 27+27\sqrt{3}+9\Big(\sqrt{3}\Big)^2+\Big(\sqrt{3}\Big)^3\\
\ \\
M = 3^3+3\cdot 3^2\sqrt{3}+3\cdot 3 \Big(\sqrt{3}\Big)^2 + \Big(\sqrt{3}\Big)^3
$$
Que, comparando com o cubo da soma, nos leva a:
$$
M = \Big(3+\sqrt{3}\Big)^3
$$
M = \Big(3+\sqrt{3}\Big)^3
$$
E para o cubo da diferença, fazemos:
$$
N = 6\Big(9-5\sqrt{3}\Big)\\
\ \\
N = 54-30\sqrt{3}\\
\ \\
N = 27+27-27\sqrt{3}-3\sqrt{3}\\
\ \\
N = 27-27\sqrt{3}+9\Big(\sqrt{3}\Big)^2-\Big(\sqrt{3}\Big)^3\\
\ \\
N = 3^3-3\cdot 3^2\sqrt{3}+3\cdot 3\Big(\sqrt{3}\Big)^2-\Big(\sqrt{3}\Big)^3\\
$$
N = \Big(3-\sqrt{3}\Big)^3
$$
N = 6\Big(9-5\sqrt{3}\Big)\\
\ \\
N = 54-30\sqrt{3}\\
\ \\
N = 27+27-27\sqrt{3}-3\sqrt{3}\\
\ \\
N = 27-27\sqrt{3}+9\Big(\sqrt{3}\Big)^2-\Big(\sqrt{3}\Big)^3\\
\ \\
N = 3^3-3\cdot 3^2\sqrt{3}+3\cdot 3\Big(\sqrt{3}\Big)^2-\Big(\sqrt{3}\Big)^3\\
$$
Que, comparando com o cuba da diferença, nos leva a:
$$N = \Big(3-\sqrt{3}\Big)^3
$$
Agora, reescrevemos a solução substituindo os valores de $M$ e $N$:
$$
x = \frac{\sqrt[3]{\Big(\sqrt{3}+3\Big)^3}}{3} +\frac{\sqrt[3]{\Big(3-\sqrt{3}\Big)^3}}{3}\\
\ \\
x = \frac{\sqrt{3}+3}{3} + \frac{3-\sqrt{3}}{3}\\
\ \\
x = \frac{\sqrt{3}-\sqrt{3}+3+3}{3}\\
\ \\
x = \frac{6}{3}\\
\ \\
x = 2
$$
\frac{x^3-2x-4}{x-2} = x^2+2x+2
$$
x = \frac{\sqrt[3]{\Big(\sqrt{3}+3\Big)^3}}{3} +\frac{\sqrt[3]{\Big(3-\sqrt{3}\Big)^3}}{3}\\
\ \\
x = \frac{\sqrt{3}+3}{3} + \frac{3-\sqrt{3}}{3}\\
\ \\
x = \frac{\sqrt{3}-\sqrt{3}+3+3}{3}\\
\ \\
x = \frac{6}{3}\\
\ \\
x = 2
$$
Assim, $x=2$ é a única raiz real da cúbica em questão, sendo outras duas imaginárias. Observando o gráfico que essa cúbica gera, podemos ver que a curva corta o eixo dos $x$ em apenas um ponto.
Para encontrar as outras duas raízes, devemos dividir o polinômio por $x-2$ ($x$ menos a raiz) para encontrarmos um polinômio de grau 2 e, assim, determinarmos as outras duas raízes. Você pode utilizar o método da chave para divisão de polinômios, encontrando:
$$\frac{x^3-2x-4}{x-2} = x^2+2x+2
$$
Para resolver a quadrática $x^2+2x+2=0$, podemos utilizar a fórmula de Bháskara:
$$
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{-2 \pm \sqrt{2^2 - 4\cdot 1 \cdot 2}}{2}\\
\ \\
x = \frac{-2\pm \sqrt{-4}}{2}\\
\ \\
x = \frac{-2\pm 2\sqrt{-1}}{2}\\
\ \\
x = -1 \pm \sqrt{-1}\\
\ \\
x = -1 \pm i\\
\ \\
x_2 = -1 + i\\
\ \\
x_3 = -1 - i
$$
x_1 = 2\ \\
x_2 = -1+i\\
x_3 = -1-i
\end{cases}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{-2 \pm \sqrt{2^2 - 4\cdot 1 \cdot 2}}{2}\\
\ \\
x = \frac{-2\pm \sqrt{-4}}{2}\\
\ \\
x = \frac{-2\pm 2\sqrt{-1}}{2}\\
\ \\
x = -1 \pm \sqrt{-1}\\
\ \\
x = -1 \pm i\\
\ \\
x_2 = -1 + i\\
\ \\
x_3 = -1 - i
$$
Assim, temos que as três raízes da equação de terceiro grau são iguais a:
\begin{cases}x_1 = 2\ \\
x_2 = -1+i\\
x_3 = -1-i
\end{cases}
Referências:
- Fundamentos de Matemática Elementar V6 - Complexos, Polinômios e Equações - Gelson Iezzi



Postar um comentário