A dedução da fórmula de Bháskara

A equação de 2º grau, muitas vezes também chamada de função quadrática, ou ainda função polinomial de 2º grau, leva esse nome porque o expoente da variável $x$ possui grau $2$.

O gráfico de uma função quadrática é uma parábola e expressa o comportamento de inúmeros fenômenos como por exemplo a trajetória de um projétil ao ser lançado, a linha descrita pela água que jorra de uma fonte ou que se projeta de uma mangueira, a estrutura que sustenta o farol de um automóvel e ainda o formato de um antena parabólica, que utiliza das propriedades da parábola para concentrar o sinal recebido em um único ponto, chamado de foco.

O objetivo desse artigo é obter a dedução para a fórmula de Bháskara, ou fórmula para a equação do segundo grau, que fornece as raízes da função quadrática em termos dos coeficientes da incógnita.

Definição

É chamada de função quadrática ou função do 2º grau toda função $f: \mathbb{R} \longrightarrow \mathbb{R}$, que, para todo número $x \in \mathbb{R}$, associa um número $ax^2+bx+c$, sendo os coeficientes $a$, $b$ e $c$ números reais, com $a \neq 0$.

A imposição de $ a \neq 0$ é a condição para que a função seja de segundo grau, pois caso $a=0$, então a função se torna de primeiro grau, uma vez que, substituindo $a=0$, obtemos $bx+c=0$.

Podemos identificar a função quadrática com um trinômio de 2º grau, de modo que podemos escrever simplesmente como:

\begin{equation*}
f(x) = ax^2+bx+c
\end{equation*}

Exemplos:

1) $f(x) = x^2-5x+6$, onde $a=1$, $b=-5$ e $c=6$;
2) $f(x) = 2x^2-2x+1$, onde $a=2$, $b=-2$ e $c=1$;
3) $f(x) = -5x^2+4x-1$, onde $a=-5$, $b=4$ e $c=-1$;
4) $f(x) = -x^2+100x$, onde $a=-1$, $b=100$ e $c=0$;
5) $f(x) = x^2-4$, onde $a=1$, $b=0$ e $c=-4$;
6) $f(x) = 3x^2$, onde $a=3$, $b=0$ e $c=0$.

Em alguns livros, a função quadrática pode aparecer como $y$ ao invés de $f(x)$:

7) $y = 3x^2+6x+2$;
8) $y = -4x^2-8x+1$;
9) $y = -2x^2+3$;
10) $y = x^2$.

Apesar de todas as funções quadráticas obedecerem à forma $ax^2+bx+c$, o que caracteriza cada uma delas, distinguindo uma da outra, são os valores atribuídos aos coeficientes $a$, $b$ e $c$. Assim, se considerarmos as funções quadráticas $f(x) = ax^2+bx+c$ e $g(x) = dx^2+ex+f$, de $\mathbb{R}$ em $\mathbb{R}$, $f(x)=g(x)$ se, e somente se, $a=d$, $b=e$ e $c=f$.

O valor de uma função quadrática em um ponto

A função quadrática expressa algebricamente o comportamento dos pontos do gráfico de uma parábola. Quando temos uma função quadrática do tipo $f(x) = ax^2+bx+c$, podemos calcular o valor da função em cada ponto, ou seja, quando atribuímos um valor específico para $x$, obtemos um valor específico para $f(x)$.

Exemplo:

Seja $f(x) = x^2-2x+3$. Vamos calcular o valor de $f(x)$ quando $x=1$, ou seja, $f(1)$. Neste caso, basta substituirmos $x$ por $1$:

\begin{equation*}
f(1) = 1^2 - 2(1) + 3\\
\ \\
f(1) = 1 - 2 + 3\\
\ \\
f(1) = 2
\end{equation*}

Se agora quisermos calcular o valor de $f(x)$ quando $x=0$, fazemos $f(0)$:

\begin{equation*}
f(0) = 0^2 - 2(0) + 3\\
\ \\
f(0) = 3
\end{equation*}

E para $x=2$, fazemos $f(2)$:

\begin{equation*}
f(2) = 2^2 -2(2) +3\\
\ \\
f(2) = 4 - 4 + 3\\
\ \\
f(2) = 3
\end{equation*}

Então, para cada valor atribuído a $x$, associa-se um valor específico para a função $f(x)$ ou para $y$, dependendo da notação utilizada. Entendida esta parte, fica fácil entender a construção de um gráfico.

Gráfico cartesiano de uma função de 2º grau

O nome da curva gerada pela função quadrática é a parábola. Para construirmos o gráfico de uma função $y=f(x) = ax^2+bx+c$, basta atribuirmos valores para $x$ e calcular o $y$ correspondente. Assim, montamos uma tabela de valores que depois podemos utilizar para construir o gráfico da parábola.

Como forma de exemplificar, vamos considerar a função $f(x) = x^2-2x-1$. Iniciamos atribuindo valores para $x$, calculando o correspondente $y$. Para construir o gráfico cartesiano, marcamos as abcissas e as ordenadas e os respectivos pontos de intersecção. A parábola é a curva que passará por essas coordenadas.

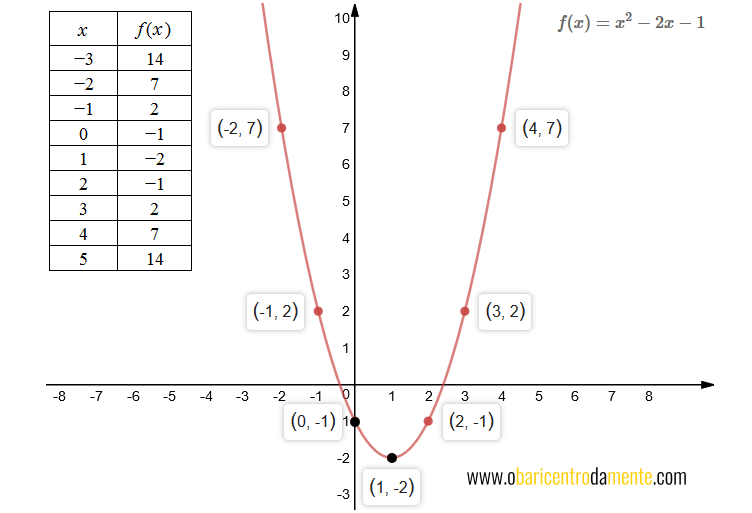
Observamos que, para esta função específica, temos que $a=1$, $b=-2$ e $c=-1$.

O coeficiente $a$ é o que define a concavidade da parábola. Se $a>0$, então a concavidade será voltada para cima; se $a<0$, então a concavidade será voltada para baixo. O coeficiente $b$ desloca a parábola horizontalmente. O coeficiente $c$ é o termo independente, ou seja, não está acompanhado pela incógnita $x$ (mas podemos pensar como $ax^2+bx^1+cx^0$ que leva a $ax^2+bx+c$. O coeficiente $c$ é o ponto em que a parábola corta o eixo dos $y$.

Forma canônica da função quadrática

A forma canônica da função quadrática permite um estudo analítico mais detalhado, de modo que poderemos deduzir a fórmula de Bháskara para encontrar as raízes de uma equação de segundo grau, ou os zeros das funções quadráticas.

O nome "forma canônica" refere-se a uma forma clássica de representar a relação, ou seja, é um modelo.

Seja uma função quadrática $f(x) = ax^2+bx+c$. Podemos reescrevê-la isolando o coeficiente $a$:

\begin{equation*}
f(x) = a\left[ \color{red}{x^2 + \frac{b}{a}x}+\frac{c}{a} \right] \tag{1}
\end{equation*}

Vejam que, as duas primeiras parcelas dentro dos colchetes, destacadas em vermelho, fazem parte do desenvolvimento do quadrado:

\begin{equation*}
\left( x+\frac{b}{2a} \right)^2 = \color{red}{x^2 + \frac{b}{a}x} + \color{blue}{\frac{b^2}{4a^2}} \tag{2}
\end{equation*}
Substituindo $(2)$ e $(1)$:
\begin{equation*}
f(x) = a\left[ \color{red}{x^2+\frac{b}{a}x}+ \color{blue}{\frac{b^2}{4a^2}-\frac{b^2}{4a^2}}+\frac{c}{a} \right] \tag{3}
\end{equation*}

Vejam que, com esta conveniente substituição, somamos um termo a mais: $\displaystyle \frac{b^2}{4a^2}$, mas logo em seguida este termo foi subtraído para manter a igualdade inalterada. Assim, reescrevemos $(3)$ como:

\begin{equation*}
f(x) = a\left[ \left(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}\right) - \frac{b^2}{4a^2}+\frac{c}{a}\right] \tag{4}
\end{equation*}
Substituindo $(2)$ em $(4)$:
\begin{equation*}
f(x) = a\left[ \left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2}{4a^2}-\frac{c}{a}\right) \right] \tag{5}
\end{equation*}
\begin{equation*}
f(x) = a\left[ \left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2-4ac}{4a^2}\right) \right] \tag{6}
\end{equation*}

A relação $(6)$ é a forma canônica da função quadrática. Mas podemos ainda representá-la da seguinte forma:

\begin{equation*}
f(x) = a \left[ \left( x+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2} \right] \tag{7}
\end{equation*}

onde $\Delta = b^2 - 4ac$ é o discriminante do trinômio do segundo grau.

Dedução da fórmula de Bháskara

A fórmula de Bháskara, ou fórmula para equação de segundo grau, é uma fórmula que resolve a equação, ou seja, a partir dela, conseguimos encontrar as raízes da equação, ou seja, obtemos os valores para a incógnita que iguale o trinômio a zero.

O termo "raízes" geralmente se refere a uma equação; já para funções utiliza-se o termo "zeros".

Seja uma função quadrática $f(x) = ax^2+bx+c$. Queremos encontrar uma fórmula que dependa dos coeficientes $a$, $b$ e $c$, de modo que $f(x)=0$.

Iniciamos com a forma canônica:

\begin{equation*}
a\left[ \left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2-4ac}{4a^2}\right) \right] = 0\\
\ \\
\left(x+\frac{b}{2a} \right)^2 = \frac{b^2-4ac}{4a^2}\\
\ \\
\sqrt{\left(x+\frac{b}{2a}\right)^2} = \sqrt{\frac{b^2-4ac}{4a^2}}\\
\ \\
x + \frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a}\\
\ \\
x = -\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a}
\end{equation*}
\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \tag{8}
\end{equation*}
onde $b^2-4ac = \Delta$.

Exemplos:

1) Vamos determinar as raízes reais da equação $x^2-5x+6=0$. Aplicando a fórmula de Bháskara, temos que:
\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{5 \pm \sqrt{(-5)^2-4 \cdot 1 \cdot 6}}{2}\\
\ \\
x = \frac{5 \pm \sqrt{25-24}}{2}\\
\ \\
x = \frac{5 \pm \sqrt{1}}{2}\\
\ \\
x = \frac{5 \pm 1}{2}\\
\ \\
x_1 = \frac{6}{2}=3\\
\ \\
x_2 = \frac{4}{2}=2
\end{equation*}

As raízes da equação são $x=2$ e $x=3$.

2) Vamos determinar as raízes reais da equação $-x^2+7x-12=0$. Aplicando a fórmula de Bháskara, temos que:

\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{-7 \pm \sqrt{7^2 - 4\cdot (-1) \cdot (-12)}}{2 \cdot (-1)} \\
\ \\
x = \frac{-1 \pm \sqrt{49-48}}{-2}\\
\ \\
x = \frac{-1 \pm 1}{-2}\\
\ \\
x_1 = \frac{-7+1}{-2} = \frac{-6}{-2} = 3\\
\ \\
x_2 = \frac{-7-1}{-2} = \frac{-8}{-2} = 4
\end{equation*}

As raízes da equação são $x-3$ e $x=4$.

3) Vamos determinar as raízes reais da equação $2x^2+3x+4$. Aplicando a fórmula de Bháskara, temos que:

\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{-3 \pm \sqrt{9-32}}{4} \\
\ \\
x = \frac{-3 \sqrt{-23}}{4}
\end{equation*}

Neste caso, não existe um número real tal que seja a raiz de um número negativo. Portanto, a raiz desta equação não pertence ao conjunto dos números reais.

4)  Vamos determinar as raízes reais da equação $x^2-6x+9=0$. Aplicando a formula de Bháskara, temos que:

\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{6 \pm \sqrt{36-36}}{2} \\
\ \\
x = \frac{6 \pm 0}{2}\\
\ \\
x_1=x_2 = 3
\end{equation*}
Neste caso, temos uma raiz dupla igual a $3$.

Números de raízes de uma equação de segundo grau

Conforme vimos nos exemplos anteriores, pode ocorrer de uma equação de segundo grau ter duas, uma ou nenhuma raiz real.

O número de raízes fica condicionado ao discriminante $\Delta = b^2-4ac$. Podemos ter três situações distintas:

• $\Delta > 0 \Rightarrow$ A equação possui 2 raízes reais distintas;
• $\Delta = 0 \Rightarrow$ A equação possui 2 raízes iguais (raiz dupla);
• $\Delta < 0 \Rightarrow$ A equação não possui raízes reais.

Significado geométrico das raízes

A interpretação geométrica das raízes são os pontos onde a parábola corta o eixo dos $x$. Então, para a parábola $y=x^2-6x+5$, temos que:

\begin{equation*}
x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{6 \pm \sqrt{36-20}}{2} \\
\ \\
x = \frac{6 \pm \sqrt{16}}{2}\\
\ \\
x_1 = \frac{6 + 4}{2}=5\\
\ \\
x_2 = \frac{6 - 4}{2}=1
\end{equation*}
Sabemos então que a parábola corta o eixo dos $x$ em $x_1=5$ e $x_2=1$. E ainda corta o eixo dos $y$ em $y=5$. Podemos atribuir alguns valores para $x$ a fim de obter uma tabela de valores para assim esboçar a parábola com mais precisão:

Apanhado geral

• O coeficiente $a$ define a concavidade da parábola;
• O coeficiente $c$ define o ponto por onde a parábola corta o eixo dos $y$;
• As raízes são os pontos por onde a parábola corta o eixo dos $x$;
• O discriminante $\Delta$ define a quantidade de raízes da equação.

Links para este artigo:

• http://bit.ly/Formula-Bhaskara
• https://www.obaricentrodamente.com/2018/04/a-deducao-da-formula-de-bhaskara.html

Referências:

• Fundamentos de Matemática Elementar V1 - Gelson Iezzi e Carlos Murakami
• Matemática, Ciência e Aplicações V1 - Gelson Iezzi et al
• Matemática, Ensino Médio V1 - Kátia Stoco Smole e Maria Ignêz Diniz
• Matemática, Contexto e Aplicações V1 - Dante
• Matemática, Volume Único - Facchini

Veja mais:

• Completando quadrados
• Demonstração dos pontos de máximo e mínimo de uma função quadrática
• Resolvendo equações quadráticas pelo método geométrico de Descartes

Softwares utilizados:

• Inkscape, Paint, Irfan View, Desmos, Excel