Construção de um triângulo equilátero através de Origami

O Origami é uma arte tradicional japonesa, praticado desde o período Edo (1603-1863), de criar figuras e formas, que consiste em dobrar o papel, sem cortá-lo ou colá-lo. Geralmente, inicia-se com um pedaço de papel quadrado, usando uma quantidade de dobras diferentes, podendo ser combinadas de diversas maneiras.

A prática do Origami traz benefícios a todos, ajuda no desenvolvimento da coordenação motora, estimula a concentração, ativa a memória, desenvolve a paciência, promove a satisfação emocional além de trazer relaxamento e satisfação. Além disso, o Origami desenvolve o pensamento lógico e matemático.

Através do Origami, podemos explorar diversos conceitos matemáticos, desde a Geometria Plana à Espacial, resolução de equações e a construção de cônicas.

Veremos neste artigo, como construir um triângulo equilátero através de Origami, utilizando poucas dobras. Em seguida veremos uma demonstração algébrica.

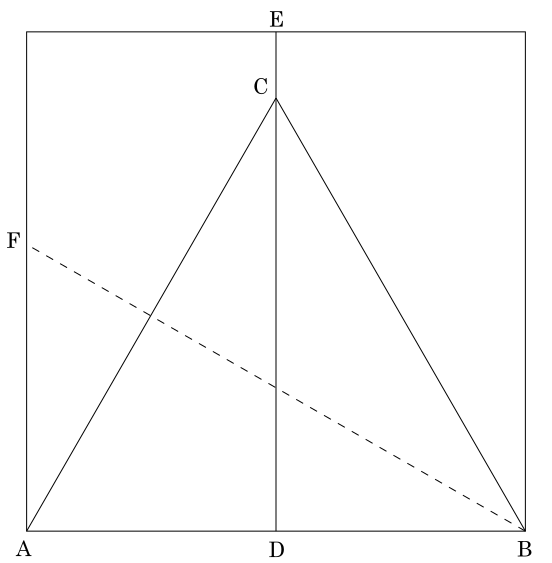
Iniciamos o Origami com um quadrado de papel, dobrando ao meio, criando a semirreta $\overline{DE}$:

Fazemos uma dobra passando por $B$ de modo que o vértice $A$ se alinhe à reta $\overline{DE}$, marcando este ponto como $C$.

O triângulo $ABC$ é o triângulo equilátero procurado:

Demonstração:

Consideremos o quadrado de lado unitário. Assim, $\overline{AB}=1$. E como a reta $\overline{DE}$ divide o quadrado ao meio, temos que $\displaystyle \overline{AD}=\overline{BD}=\frac{1}{2}$. O segmento $\overline{BC}$ é a imagem de $\overline{AB}$, e também mede $1$. 

Como o triângulo $BDC$ é reto em $D$, podemos aplicar o teorema de Pitágoras:

\begin{equation*}
\overline{BD}^2 + \overline{DC}^2 = \overline{BC}^2\\
\ \\
\left( \frac{1}{2}\right)^2 + \overline{DC}^2 = 1^2\\
\ \\
\overline{DC}^2 = 1 - \frac{1}{4}\\
\ \\
\overline{DC}^2 = \frac{3}{4}\\
\ \\
\overline{DC} = \frac{\sqrt{3}}{2}
\end{equation*}

O segmento $\overline{DC}$ é a altura do triângulo $ABC$.

Da mesma forma, aplicamos o teorema de Pitágoras no triângulo $ADC$:

\begin{equation*}
\overline{AD}^2 + \overline{DC}^2 = \overline{AC}^2\\
\ \\
\left(\frac{1}{2}\right)^2 + \left( \frac{\sqrt{3}}{2}\right)^2 = \overline{AC}^2\\
\ \\
\frac{1}{4} + \frac{3}{4} = \overline{AC}^2\\
\ \\
\overline{AC} = 1
\end{equation*}

O segmento $\overline{AC}=1$ se e somente se o segmento $\overline{BC}=1$, uma vez que o segmento $\overline{AB}=1$ por definição.

Links para este artigo:

• http://bit.ly/Origami-Triangulo-Equilatero
• https://www.obaricentrodamente.com/2018/04/construcao-triangulo-equilatero-origami.html

Referências:

• Origami: História de uma geometria axiomática - Liliana C. N. Monteiro
• Guia infantil - Origami 
• Origami no Wikipédia

Veja mais:

• Construção de sólidos platônicos em Origami no blog o Prof. Edigley Alexandre
• Relações métricas no triângulo retângulo 
• Pontos notáveis de um triângulo

Softwares utilizados:

• Inkscape