O número de ouro, representado pela letra grega $\varphi$, é uma das soluções de uma equação quadrática obtida através da análise da proporção áurea.
Antes de seguirmos, vamos entender o que é a proporção áurea.
Definição de proporção áurea
A proporção áurea é uma razão entre duas medidas resultando em uma constante real, algébrica e irracional, denotada por $\varphi$ e que vale aproximadamente $1,618 \cdots$
Segundo a história, a letra $\varphi$ foi atribuída ao número de ouro por conta do matemático e arquiteto grego Phídeas, que acredita-se que tenha utilizada a proporção áurea pela primeira vez na construção do Parthenon, no século V a.C..
Como obter a proporção áurea
A proporção áurea é uma razão entre duas medidas que resulta no número de ouro. A princípio, podemos utilizar um segmento de reta dividido em um ponto, de tal forma que satisfaça a definição;
Assim:
$$\frac{AB}{AC} = \frac{AC}{CB} = \varphi = 1,618 \cdots
$$
Outra forma de obter a proporção áurea é através de um retângulo, de modo que a razão entre dois de seus lados adjacentes satisfaça a definição:
Assim:
$$\frac{AB}{BC} = \varphi
$$
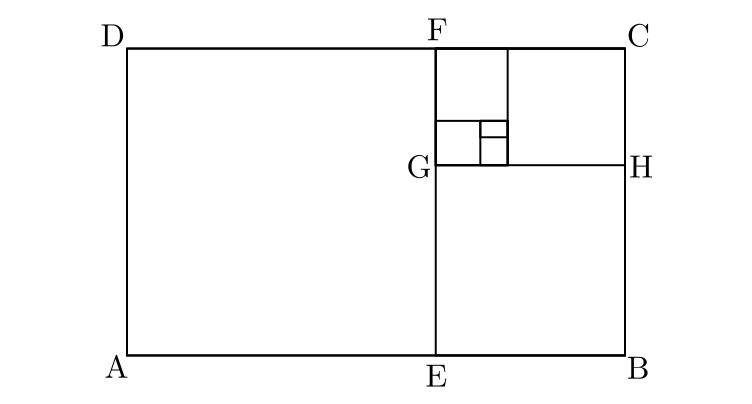
Podemos continuar dividindo o retângulo em proporção áurea:
Desta forma, obtemos:
$$\frac{AB}{BC} = \frac{BC}{CF} = \frac{CF}{FG} = \cdots = \varphi
$$
A equação do número de ouro
Para encontrarmos a equação do número de ouro, vamos considerar um retângulo cujos lados encontram-se em proporção áurea:
Assim, temos que:
$$\frac{a+b}{a} = \frac{a}{b} = \varphi \tag{1}
$$
Da parte direita da equação $(1)$, temos:
$$\frac{a}{b} = \varphi
$$
Logo:
$$a = b\ \varphi \tag{2}
$$
Agora, podemos substituir a relação $(2)$ na parte esquerda da relação $(1)$:
$$
\frac{a+b}{a} = \frac{a}{b}\\
\ \\
\frac{b\varphi +b}{b \varphi} = \frac{b \varphi}{b}\\
\ \\
\frac{b (\varphi + 1)}{b \varphi} = \varphi\\
\ \\
\frac{\varphi + 1}{\varphi} = \varphi\\
\ \\
\varphi + 1 = \varphi^2
$$
\frac{a+b}{a} = \frac{a}{b}\\
\ \\
\frac{b\varphi +b}{b \varphi} = \frac{b \varphi}{b}\\
\ \\
\frac{b (\varphi + 1)}{b \varphi} = \varphi\\
\ \\
\frac{\varphi + 1}{\varphi} = \varphi\\
\ \\
\varphi + 1 = \varphi^2
$$
E finalmente obtendo:
$$\varphi^2 - \varphi - 1 = 0 \tag{3}
$$
A relação acima é a equação que gera o número de ouro. Vejam que é uma equação do segundo grau, cuja variável é $\varphi$, e que podemos resolvê-la utilizando a fórmula de Bháskara:
$$\varphi = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
\varphi = \frac{-(-1)\pm \sqrt{(-1)^2-4\cdot 1 \cdot (-1)}}{2\cdot 1}\\
\ \\
\varphi = \frac{1 \pm \sqrt{1+4}}{2}\\
\ \\
\varphi = \frac{1\pm \sqrt{5}}{2}
$$
A equação nos fornece duas soluções:
$$\varphi_1 = \frac{1+\sqrt{5}}{2} = 1,618 \cdots\\
\ \\
\varphi_2 = \frac{1-\sqrt{5}}{2} = -0,618 \cdots
$$
A solução que nos interessa é a positiva. Então:
$$\varphi = \frac{1+\sqrt{5}}{2} = 1,618\cdots
$$
Papel de parede sobre o numero de ouro:
Acesse o blog do Professor Edigley Alexandre e baixe este lindo papel de parede:







Sobre o papel de parece, depois de algum tempo eu comecei a achar eles feios. kkkk
ResponderExcluirÉ que você está muito exigente, cara! É muito bonito!
Excluir