Sangaku são tábuas comemorativas contendo problemas geométricos japoneses. Eram confeccionadas em madeira, e penduradas nos recintos dos templos budistas e santuários xintoístas como forma de oferendas aos Kami e Budas durante o período Edo. As tábuas eram desafios aos congregantes ou apenas demonstrações das soluções para as questões.
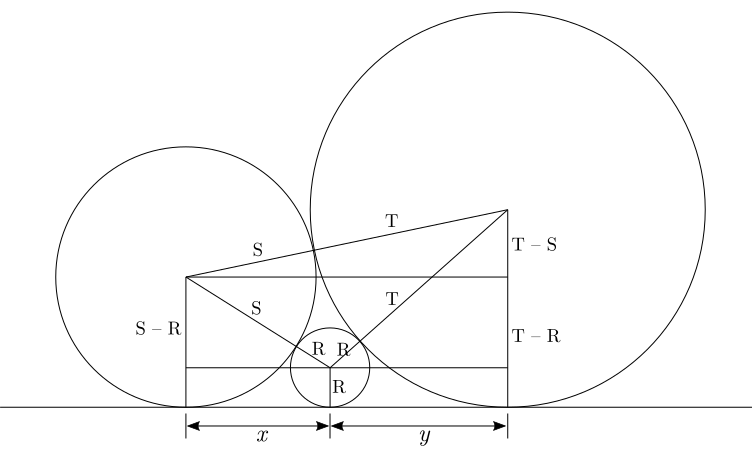
Um problema típico do quebra-cabeça Sangaku é o que aparecem três círculos tangentes dois a dois, sendo os três tangentes a uma reta. Este problema apareceu em uma tábua de 1824 na província de Gunma e essencialmente diz que, dados dois círculos grandes externos, calcular o raio do círculo pequeno entre eles.
Denotamos por $x$ e $y$ as distâncias entre as retas verticais que cruzam os centros dos círculos de raios $R$ e $S$ e raios $R$ e $T$, respectivamente. Com isso, obtemos três triângulos retângulos distintos:
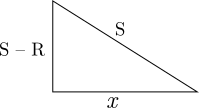
Aplicamos o teorema pitagórico:
$$(S-R)^2 + x^2 = (R+S)^2\\
\ \\
S^2-2RS+R^2 + x^2 = S^2+2RS+R^2\\
\ \\
x^2=S^2+2RS+R^2-S^2+2RS-R^2\\
\ \\
x^2 = 4RS
$$
Extraindo a raiz, obtemos:
$$x = 2\sqrt{RS} \tag{1}
$$
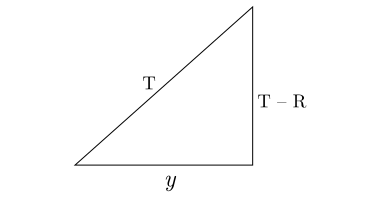
Aplicamos o teorema pitagórico:
$$(T-R)^2+y^2 = (R+T)^2\\
\ \\
T^2-2RT+R^2 + y^2 = R^2+2RT+T^2\\
\ \\
y^2 = R^2+2RT+T^2-T^2+2RT-R^2\\
\ \\
y^2 = 4RT
$$
Extraindo a raiz:
$$y = 2\sqrt{RT} \tag{2}
$$
Aplicamos o teorema pitagórico:
$$(T-S)^2 + (x+y)^2 = (S+T)^2\\
\ \\
T^2-2ST+S^2 + (x+y)^2 = S^2+2ST+T^2\\
\ \\
(x+y)^2 = S^2+2ST+T^2-T^2+2ST-S^2\\
\ \\
(x+y)^2 = 4ST
$$
Extraindo a raiz:
$$
x+y = 2\sqrt{ST} \tag{3}
$$Substituindo $(1)$ e $(2)$ em $(3)$, obtemos:
$$x+y = 2\sqrt{ST} \tag{3}
$$Substituindo $(1)$ e $(2)$ em $(3)$, obtemos:
2\sqrt{RS} + 2\sqrt{RT} = 2\sqrt{ST}\\
\ \\
2\left(\sqrt{RS}+\sqrt{RT}\right) = 2\sqrt{ST}\\
\ \\
\sqrt{RS}+\sqrt{RT} = \sqrt{ST}
$$
Dividimos ambos os membros da equação por $\sqrt{R}\sqrt{S}\sqrt{T}$:
$$\frac{\sqrt{RS}}{\sqrt{R}\sqrt{S}\sqrt{T}}+\frac{\sqrt{RT}}{\sqrt{R}\sqrt{S}\sqrt{T}} = \frac{\sqrt{ST}}{\sqrt{R}\sqrt{S}\sqrt{T}}\\
$$
E por fim, obtemos:
$$
\frac{1}{\sqrt{T}} + \frac{1}{\sqrt{S}} = \frac{1}{\sqrt{R}} \tag{4}
$$
R = \frac{1}{\displaystyle \left( \frac{1}{\sqrt{S}} + \frac{1}{\sqrt{T}} \right)^2} \tag{5}
$$
\frac{1}{\sqrt{T}} + \frac{1}{\sqrt{S}} = \frac{1}{\sqrt{R}} \tag{4}
$$
A equação acima relaciona os três raios das circunferências. Com um pouco de álgebra podemos isolar a variável $R$ para que ele seja determinado em função dos outros dois:
$$R = \frac{1}{\displaystyle \left( \frac{1}{\sqrt{S}} + \frac{1}{\sqrt{T}} \right)^2} \tag{5}
$$
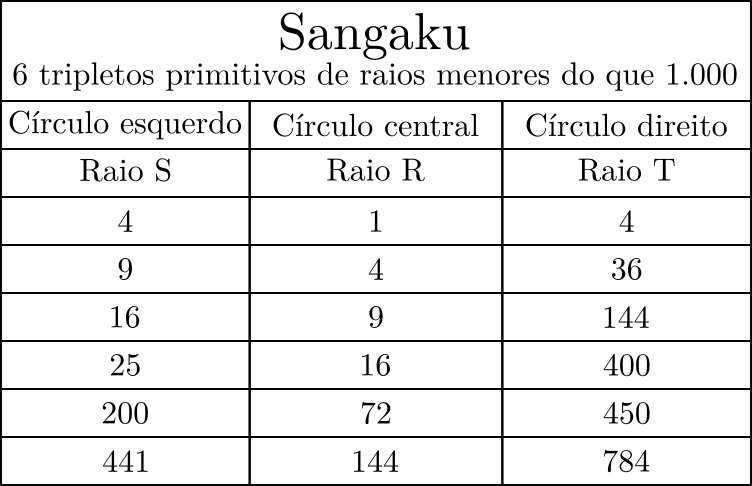
Podemos, assim, criar uma tabela com os 6 tripletos primitivos de raios menores do que 1.000:




Postar um comentário