Al-Khwārizmī $(780-850\ d.C.)$ foi o pai da álgebra e o primeiro a escrever um tratado detalhado sobre operações com números decimais. Al-Kasi foi o primeiro matemático a formalizar uma teoria com frações decimais e a noção de número decimal em seu livro "Chave da Aritmética".
François Viéte $(1540-1603)$ apresentou os números decimais em diferentes configurações. Simon Stevin $(1548-1620)$ sugeriu simplificações de cálculos com números decimais. Em seu livro "O décimo", apresenta uma nova notação para representação decimal, como se fossem números inteiros. Por exemplo, o número $6,987$ era representado como $6(0)\ 9(1)\ 8(2)\ 7(3)$, o que seria lido como: seis comunzos, nove primeiras, oito segundas e sete terceiras. Essa representação logo seria substituída pela notação atual com a vírgula separando a parte inteira da parte decimal.
François Viéte $(1540-1603)$ apresentou os números decimais em diferentes configurações. Simon Stevin $(1548-1620)$ sugeriu simplificações de cálculos com números decimais. Em seu livro "O décimo", apresenta uma nova notação para representação decimal, como se fossem números inteiros. Por exemplo, o número $6,987$ era representado como $6(0)\ 9(1)\ 8(2)\ 7(3)$, o que seria lido como: seis comunzos, nove primeiras, oito segundas e sete terceiras. Essa representação logo seria substituída pela notação atual com a vírgula separando a parte inteira da parte decimal.
Os números decimais são aqueles que possuem uma parte inteira e outra fracionária, separadas por uma vírgula (chamada de vírgula decimal) onde a parte inteira fica à esquerda da vírgula, enquanto a parte fracionária à direita.
Um exemplo de um número decimal é o número $2,35$. A parte inteira (à esquerda da vírgula) é o algarismo $2$; já a parte fracionária fica à direita da vírgula. Assim, podemos reescrever este número como:
$$2, 35 = 2 + \frac{3}{10} + \frac{5}{100}\\
\ \\
2,35= 2 + 0,3 + 0,05
$$
O número $2$ representa a parte inteira e o $0,35$ representa a parte decimal.
Então, de uma forma mais informal, podemos fazer nossa primeira definição de números decimais:
Definição 1: Números decimais são aqueles que possuem uma vírgula separando a parte inteira da parte fracionária.
Até é verdade, mas é somente isso?
Tomando o exemplo anterior, como temos frações envolvidas, logo já pensamos no conjunto dos números racionais, representado por $\mathbb{Q}$, apesar de que o número inteiro $2$ também pode ser representado em forma de uma fração. E ainda podem ser positivos ou negativos. Sendo assim, podemos melhorar a definição 1:
Definição 2: Números decimais são números pertencentes ao conjunto dos números racionais $(\mathbb{Q})$, não inteiros, onde a vírgula decimal separa a parte inteira da parte fracionária.
Podemos ver outros exemplos:
O número $1,5$ representa um inteiro e cinco décimos. Pode ser representado com a soma:
$$1,5 = 1 + \frac{5}{10}\\
\ \\
1,5 = 1 + 0,5
$$
O número $4,63$ representa quatro inteiros, seis décimos e três centésimos. Pode ser representado pela soma:
$$4,63 = 4 + \frac{6}{10} + \frac{3}{100}\\
\ \\
4,63 = 4 + 0,6 + 0,03
$$
O número $8,932$ representa oito inteiros, nove décimos, três centésimos e dois milésimos. Pode ser representado pela soma:
$$8,932 = 8 + \frac{9}{10} + \frac{3}{100} + \frac{2}{1.000}\\
\ \\
8,932 = 8 + 0,9 + 0,03 + 0,002
$$
Como pudemos ver, todo número decimal conseguimos reescrevê-lo como a soma de um número inteiro com uma soma de frações, utilizando como denominadores, potências de $10$, onde estas frações representam a parte à direita da vírgula, pertencentes às décimas.
Cada fração, cujos denominadores são potências de $10$, assumem uma posição ocupada após a vírgula e essa posição recebe o nome de casa decimal. Por exemplo, o número $1,2345$ possui quatro casas decimais e o algarismo $3$ está localizado na segunda casa decimal.
Os exemplos acima são de números decimais finitos. Recebem essa terminologia porque as casas decimais são finitas, ou seja sabemos a quantidade exata de casas decimais e se transformados em uma soma de frações decimais, obtemos uma soma com número finito de parcelas.
No entanto, existem números decimais infinitos, onde as casas decimais são infinitas. Poderíamos adotar a seguinte definição provisória: Uma classe desses números decimais infinitos são aqueles obtidos pelo quociente entre dois números, ou seja, existe uma fração do tipo $p/q$, com $q \neq 0$.
Sendo assim, melhoramos ainda mais nossa definição sobre números decimais:
Definição 3: Números decimais são números não inteiros, pertencentes ao conjunto dos números racionais $(\mathbb{Q})$, que podem ser expressos sob a forma de fração $p/q$, sendo $p$ e $q$ inteiros, primos entre si e $q \neq 0$.
O que aconteceria se não incluirmos a exigência que os inteiros $p$ e $q$ sejam primos entre si?
O quociente dessas frações pode resultar em decimais finitos ou decimais infinitos periódicos. Neste último caso, são chamadas de dízimas periódicas, pois apresentam uma quantidade infinita de algarismos decimais que, a partir de um determinado algarismo, passam a repetir-se em grupos de um ou mais algarismos. Esses grupos são denominados períodos e o comprimento desses períodos são dados pela quantidade e algarismos que os formam.
Essas frações podem gerar dois tipos de dízimas periódicas: as dízimas periódicas simples, onde o período aparece imediatamente após a vírgula e as dízimas periódicas compostas, onde entre a vírgula e o período existe um ou mais algarismos que não se repetem e são chamados de parte não-periódica ou anti-período.
Como exemplo de uma dízima periódica simples, temos a fração geratriz:
$$\\frac{1}{9} = 0,111111 \cdots
$$
Vejam que neste caso, o algarismo $1$ se repete indefinidamente imediatamente à direita da vírgula decimal. A parte inteira vale $0$ e o período é igual a $1$.
Outro exemplo de dízima periódica simples, temos:
$$\frac{7}{3} = 2,333333 \cdots
$$
Neste caso, o algarismo $3$ se repete indefinidamente. A parte inteira é igual a $2$ e o período é igual a $3$.
Como exemplo de uma dízima periódica composta, temos a fração geratriz:
$$\frac{61}{495} = 0,1232323 \cdots
$$
Vejam que a parte inteira é igual a $0$, a parte não-periódica é o algarismo $1$ e o período é igual a $23$.
Outro exemplo de dízima periódica composta é a dado pela fração:
$$\frac{123}{56} = 2,196428571428571428571 \cdots
$$
Neste caso, a parte inteira vale $2$, a parte não-periódica vale $196$ e o período é igual a $428571$.
Apesar de já termos cercado grande parte dos número decimais, parece haver alguns outros tipos que merecem nossa atenção.
Se tomarmos um quadrado de lado igual a $1$, sua diagonal valerá $\sqrt{2}$. Essa raiz não pode ser expressa sob a forma de uma fração do tipo que vimos nos tópicos acima, ou seja, não existe um quociente entre números inteiros que resulte a raiz quadrada de dois. Isso também ocorre com outras raízes. Vejamos algumas delas:
$$\sqrt{2} = 1,41421356237309504880168 \cdots\\
\ \\
\sqrt{5} = 2,23606797749978969640917 \cdots\\
\ \\
\sqrt{7} = 2,64575131106459059050161 \cdots
$$
Podemos observar que na expansão decimal não há um período, ou seja, não há algarismos que se repetem indefinidamente.
É possível demonstrar que é impossível representar essas frações como a razão entre dois números inteiros primos entre si. Veja a demonstração no artigo Demonstração de número irracional.
É possível demonstrar que é impossível representar essas frações como a razão entre dois números inteiros primos entre si. Veja a demonstração no artigo Demonstração de número irracional.
No entanto, podemos representar a parte decimal como uma soma infinita de frações, cujos denominadores são potências de dez:
$$\sqrt{2} = 1 + \frac{4}{10} + \frac{1}{100} + \frac{4}{1000} + \frac{2}{10000} + \cdots
$$
Esses números não se encaixam no conjunto dos números racionais $(\mathbb{Q})$, pois não podem ser expressos sob a forma de frações. Sendo assim, um outro conjunto numérico foi criado para estes números especiais e foi chamado de conjunto dos números irracionais $(\mathbb{I})$.
Os números irracionais ainda podem ser classificados em algébricos e transcendentes.
Um número irracional algébrico é todo número que é solução de uma equação polinomial, cujos coeficientes são números inteiros. Como exemplo de um número irracional algébrico, temos o número $\displaystyle \frac{\sqrt[3]{3}}{2}$ que é uma das raízes para a equação:
$$8x^3-3=0
$$
O número de ouro, representado pela letra grega $\varphi$, e que vale $1,618\cdots$, é uma constante irracional algébrica, pois é solução da equação:
$$\varphi^2-\varphi-1 = 0\\
\ \\
\varphi = \frac{1+\sqrt{5}}{2}\\
\ \\
\varphi = 1,618 \cdots
$$
Um número irracional transcendente é todo número que não é solução de uma equação polinomial. Como exemplos temos duas constantes famosas e importantes: o número $\pi$, que é a razão entre o perímetro e o diâmetro de qualquer circunferência, e o número de Neper, representado pela letra $e$:
$$\pi = 3,141592653589 \cdots\\
\ \\
e = 2,718281828459 \cdots
$$
Nos vemos forçados a construir uma definição um pouco mais abrangente do que aquela feita na definição 3, de modo a incluir os números irracionais. Os conjuntos dos números racionais e irracionais são distintos, um não contém o outro, no entanto, ambos são subconjuntos do conjunto dos números reais $\mathbb{R}$. Sendo assim, chegamos a uma nova definição para números decimais:
Definição 4: Números decimais são números não inteiros, pertencentes ao conjunto dos números reais $\mathbb{R}$.
Com esta definição, abrangemos todos os casos que envolvem os números decimais pertencentes aos reais. Cada um dos casos descritos acima tem suas peculiaridades e por isso devemos nos atentar aos casos particulares. Abaixo podemos ver uma classificação dos números decimais:
Também é relevante observar que todo número racional é algébrico e que todo número transcendente é irracional, embora nem todo irracional seja transcendente.
De acordo com (Eves, p. 645) a primeira demonstração de que $\pi$ é transcendente foi dada por F. Lindemann (1852,1939) em 1882. O fato de $\pi$ ser transcendente assegura que o problema da quadratura não possui solução por instrumentos euclidianos (Eves, p. 146), uma questão que desafiou as grandes mentes matemáticas desde os gregos só foi ser demonstrada como impossível de ser resolvida no século XIX, mais de 2000 anos depois.
Este é um exemplo de como uma área da Matemática, no caso a geometria plana, pode se conectar com outras áreas da Matemática, aparentemente sem uma conexão imediata.
Conseguir construir conexões entre áreas distintas da Matemática é tão importante para os pesquisadores matemáticos quanto para os aprendizes da Matemática. Ao conectar áreas distintas, podemos “transferir tecnologia” levando Teoremas e ferramentas de uma área para a outra e depois, trazendo a solução “de volta”. Quer outro exemplo? A geometria analítica.
Leitura de números decimais:
Para lermos corretamente um número decimal, temos que entender como são formados. O sistema decimal é um sistema posicional, onde cada algarismo ocupa uma posição e recebe um nome específico.
Como já vimos no exemplos anteriores, cada algarismo pode ser escrito como uma soma de frações, cujos denominadores são potências de dez. Vejamos alguns exemplos:
$1,234 \longrightarrow $ Lê-se: Um inteiro e duzentos e trinta e quatro milésimos.
$$1,234 = 1 + \frac{2}{10} + \frac{3}{100} + \frac{4}{1000}\\
\ \\
1,234 = 1 + \frac{234}{1000}
$$
$0,2 \longrightarrow $: Lê-se: Dois décimos.
$$0,2 = \frac{2}{10}
$$
$6,72 \longrightarrow$ Lê-se: Seis inteiros e setenta e dois centésimos.
$$6,72 = 6 + \frac{7}{10} + \frac{2}{100}
$$
Na prática, não costumamos ler assim os números decimais. Talvez por não praticarmos a leitura correta, mas acredito que seja simplesmente para economizar tempo. Para os mesmos exemplos acima, costumamos ler da seguinte forma:
$1,234 \longrightarrow$ Lemos: Um vírgula duzentos e trinta e quatro. Ou ainda, um vírgula dois três quatro.
$0,2 \longrightarrow$ Lemos: zero vírgula dois.
$6,72 \longrightarrow$ Lemos: seis vírgula setenta e dois, ou ainda, seis vírgula sete dois.
► Sugiro a leitura do artigo Como escrever números decimais por extenso no blog Como escreve da Marilucia Santos, pois possui mais detalhes.
► Sugiro a leitura do artigo Como escrever números decimais por extenso no blog Como escreve da Marilucia Santos, pois possui mais detalhes.
Onde encontrar números decimais no dia-a-dia:
No mundo real, os números decimais estão por toda a parte. Em unidades monetárias, medidas de comprimento, volume, peso, área, coordenadas geográficas, temperatura, velocidade, tempo, ...
► Unidade monetária
No Brasil, a unidade monetária é o Real, representado por $R\$$. Todos os produtos e serviços possuem um preço, que podem variar de centavos de Real a milhares ou milhões de Reais.
No caso de unidade monetária, a parte inteira equivale aos Reais e a parte decimal são os centavos de Real. Recebe esse nome porque $1$ Real foi dividido em $100$ partes, de modo que $1$ centavo equivale à $1$ centésimo de Real, ou seja, $1$ centavo de Real.
A imagem acima mostra um montante de $R\$\ 39,35$. Lemos: Trinta e nove reais e trinta e cinco centavos. O $39$ é a parte inteira e o $35$ é a parte decimal.
► Unidade de comprimento:
No Brasil, a unidade de medida de comprimento é o metro $(m)$. Os múltiplos e submúltiplos são potências de $10$ e são utilizados para representar comprimentos, ou seja, distâncias entre dois pontos.
No caso de unidade monetária, a parte inteira equivale aos Reais e a parte decimal são os centavos de Real. Recebe esse nome porque $1$ Real foi dividido em $100$ partes, de modo que $1$ centavo equivale à $1$ centésimo de Real, ou seja, $1$ centavo de Real.
A imagem acima mostra um montante de $R\$\ 39,35$. Lemos: Trinta e nove reais e trinta e cinco centavos. O $39$ é a parte inteira e o $35$ é a parte decimal.
► Unidade de comprimento:
No Brasil, a unidade de medida de comprimento é o metro $(m)$. Os múltiplos e submúltiplos são potências de $10$ e são utilizados para representar comprimentos, ou seja, distâncias entre dois pontos.
Por exemplo, a medida da altura de uma pessoa, geralmente é dado em metros e centímetros. Vemos na imagem abaixo algumas medidas das alturas médias de homens e mulheres de alguns países.
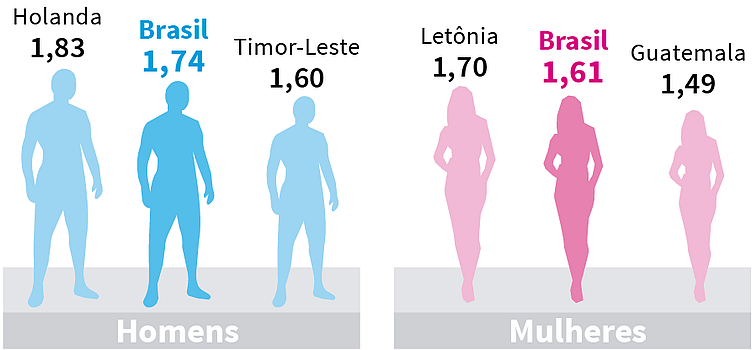
A altura média do Homem brasileiro é de $1,74\ m$, ou seja, um metro e setenta e quatro centímetros. A altura média da Mulher brasileira é de $1,61\ m$, ou seja, um metro e sessenta e um centímetros.
Para a medida de distâncias, desde que não sejam curtas, utiliza-se o quilômetro como unidade de medida. Pesquisando a distância entre a cidade de São Paulo, SP e Salvador, BA, o Google forneceu uma distância de $1.973,7\ km$, mil novecentos e setenta e três vírgula sete quilômetros. Isso para um percurso de automóvel.
Vejam que a parte inteira vale $1.973$ e a parte decimal vale $0,7\ km$, ou seja, sete décimos de quilômetro, ou seja, $700$ metros. Como a distância é muito grande, não é necessário maior precisão na escrita, como centímetros, por exemplo.
► Unidades de volume:
O volume é definido como o espaço ocupado por um corpo. Pelo Sistema Internacional de Unidades, a unidade de medida de volume é o metro cúbico $m^3$. A capacidade é o volume interno de um corpo, simbolizado por $l$ ou $L$.
Vale lembrar que $1\ m^3$ equivale a $1.000\ L$ e desta relação podemos calcular qualquer múltiplo ou submúltiplo.
Em nosso cotidiano é muito comum encontrarmos embalagens de produtos com suas capacidades dadas em litros, ou em seu submúltiplo, o mililitro.
No exemplo da imagem abaixo, podemos encontrar embalagens de água mineral com diversas capacidades: $20\ L$, $10\ L$, $6\ L$, $2\ L$, $1,5\ L$, $1\ L$, $510\ mL$, $300\ mL$, $250\ mL$, $200\ mL$, $120\ mL$.
Não vou estender mais com exemplos, pois acredito que foi possível ilustrar a importância de sabermos identificar e compreender os números decimais ao nosso redor. Acredite, a Natureza não é exata.
► Outras medidas:
O peso de pessoas ou objetos são produtos de sua massa pela ação da gravidade. A unidade de medida padrão é o quilograma $(kg)$. Múltiplos e submúltiplos também são utilizados e a precisão depende da utilidade. Para medir o peso de uma pessoa, geralmente usa-se precisão de décimos, por exemplo $65,3\ kg$, ou seja sessenta e cinco vírgula três quilos, ou ainda, sessenta e cinco quilos e trezentos gramas.
A temperatura também é dada em números decimais, por exemplo uma temperatura de $23,7^{\circle} C$, ou seja, vinte e três vírgula sete graus Celsius, ou ainda, vinte e três graus Celsius e sete décimos.
Coordenadas geográficas também podem ser expressas em graus decimais. Por exemplo, o arquipélago de Tristão da Cunha está localizado no sul do Oceano Atlântico e é o local habitado mais isolado do mundo. Suas coordenadas geográficas são: $-37.1134402,-12.3250074$.
Ficarei por aqui com exemplos para não estender demais este artigo, mas devemos ficar cientes que existe uma infinidade de aplicações, seja na matemática abstrata ou aplicada ou ainda no nosso cotidiano, mesmo que não esteja explícito.
Links para este artigo:
- http://bit.ly/numeros-decimais
- https://www.obaricentrodamente.com/2018/12/classificacao-dos-numeros-decimais.html
Referências:
- Simon Stevin e os números decimais - Sandy C. Dias
- Números decimais: Dificuldades e propostas para o ensino e o aprendizado de alunos de 5ª a 6ª série - Carlos E. Espinosa
Postar um comentário