Como determinar a intersecção de duas retas

A intersecção de duas retas ocorre quando elas se cruzam em um único ponto. A condição para que ocorra é que as duas retas não sejam paralelas. Dizemos que duas retas são concorrentes se, e somente se, possuírem apenas um ponto em comum.

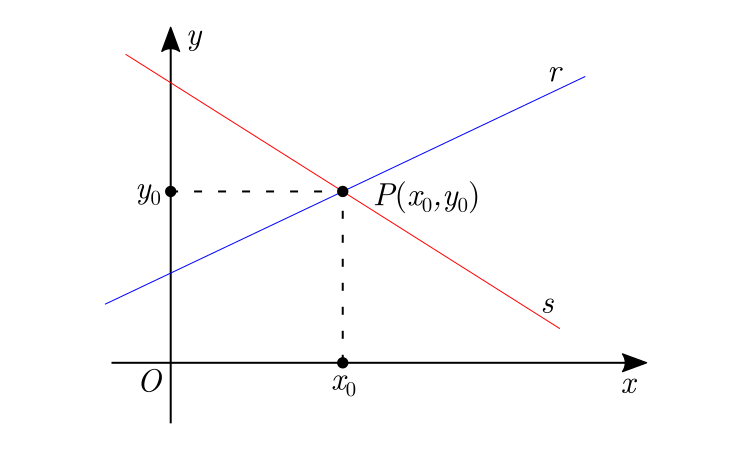
Para encontrarmos as coordenadas $(x,y)$ do ponto de intersecção das duas retas, é necessário resolvermos o sistema composto pelas equações que descreve cada uma delas. Portanto, a solução do sistema é o ponto $P(x_0,y_0)$ que satisfaz ambas as equações.

Sejam duas retas $r$ e $s$, cujas equações em sua forma geral são dadas por:

\begin{cases}
r: \quad a_1x + b_1y + c_1 = 0\\

s: \quad a_2x + b_2y + c_2 = 0
\end{cases}

Ao encontrarmos a solução desse sistema, obteremos o ponto de intersecção entre as duas retas.

Graficamente, teremos um problemas semelhante:

Exemplo 1:

Determinar o ponto de de intersecção entre as retas $r$ e $s$ representadas pelas equações:

\begin{cases}
r: \quad & x & - & y & + & 1 & = & 0\\

s: \quad & 2x & + & y & - & 2 & = & 0
\end{cases}

Existem métodos diferentes para resolver um sistema linear. Temos que tentar utilizar aquele que for menos trabalhoso. Isso somente será possível com a prática. Neste caso, podemos utilizar o método da soma, a fim de eliminar a incógnita $y$. Somamos, então, as equações $(1)$ e $(2)$:

\begin{matrix}
x & - & y & + & 1 & = & 0 & \quad (1) \\
2x & + & y & - & 2 & = & 0 & \quad(2) \\
\hline
3x & + & 0 & -& 1 & = & 0 &
\end{matrix}

Daqui, temos que:

$$
3x-1=0\\

3x=1\\

x=\frac{1}{3}
$$

Podemos substituir o valor obtido de $x$ na equação $(1)$ ou na equação $(2)$ para encontrar o valor de $y$. Vamos fazer a substituição na equação $(2)$:

$$
2x+y-2=0\\

2\left(\frac{1}{3}\right) + y - 2 = 0\\

\frac{2}{3} + y - 2 =0\\

y = 2-\frac{2}{3}\\

y = \frac{4}{3}
$$

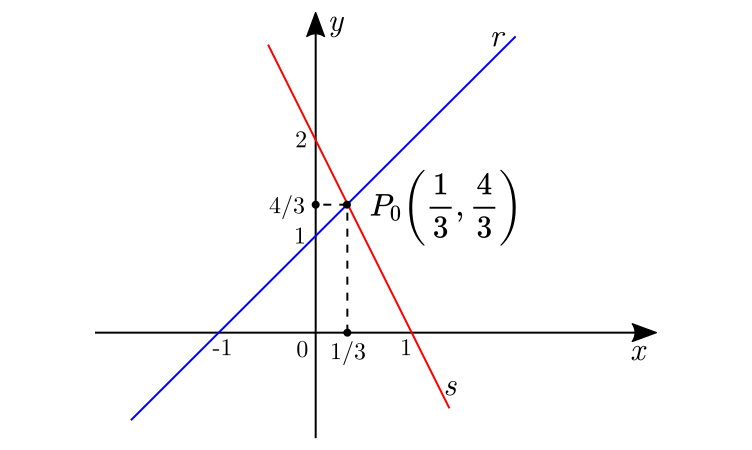
Assim, a intersecção das duas retas se dá pelo no ponto $\displaystyle P\left(\frac{1}{3}, \frac{4}{3}\right)$.

Para criarmos um gráfico que represente as retas, podemos utilizar um software (como o Geogebra) ou esboçarmos manualmente. Dois pontos definem uma reta , de modo que precisamos encontrar dois pontos para traçarmos a reta. Podemos atribuir um valor arbitrário para $x$ e assim obter $y$. Mas na maioria dos casos, é mais fácil atribuir $0$ para $x$ e depois $0$ para $y$.

Para a reta $r$:

\begin{matrix}
x-y+1=0 & \qquad \text{e} \qquad & x-y+1=0\\

0-y+1=0 & & x-0+1=0\\

y = 1 & & x = -1 \\

P_1(0,1) & & P_2(-1,0)
\end{matrix}

Para a reta $s$:

\begin{matrix}
2x+y-2=0 & \qquad \text{e} \qquad & 2x+y-2=0\\

2\cdot 0+y-2=0 & & 2x+0-2=0\\

y = 2 & & x = 1\\

P_3(0,2) & & P_4(1,0)
\end{matrix}

Graficamente:

Exemplo 2:

Determinar o ponto de de intersecção entre as retas $r$ e $s$ representadas pelas equações:

\begin{cases}
r: \quad & x & - & 5y &  = & 14\\
s: \quad & 3x & + & 2y &  = & -9
\end{cases}

Para resolver o sistema, podemos isolar $x$ na primeira equação:

\begin{cases}
x & - & 5y & = & 14 & \quad (1) \\
3x & + & 2y & = & -9 & \quad(2) \\
\end{cases}

Fazemos:

$$
x-5y=14\\
x=14+5y
$$

Substituímos $x$ na segunda equação:

$$
3x+2y=-9\\
3(14+5y)+2y=-9\\
42+15y+2y=-9\\
17y=-51\\
y=-3
$$

Agora, substituímos o valor de $y$ na primeira equação para obtermos o valor de $x$:

$$
x-5y=14\\
x-5(-3)=14\\
x+15=14\\
x=-1
$$

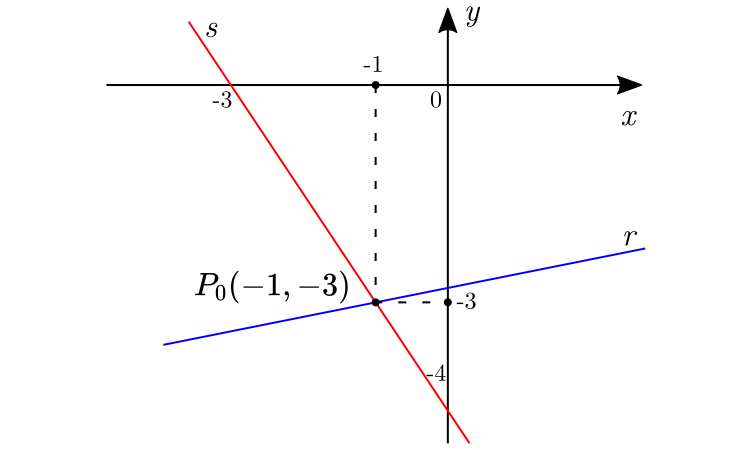
Assim, as retas $r$ e $s$ interceptam-se no ponto $P(-1,-3)$.

Graficamente, temos:

Exemplo 3:

Determinar o ponto de de intersecção entre as retas $r$ e $s$ representadas pelas equações:

\begin{cases}
r: \quad & 2x & - & y & = & -2\\
s: \quad & x & + & 2y & = & -6
\end{cases}

Podemos isolar $y$ na primeira equação e substituir na segunda, mas vamos resolver de outro modo, multiplicando a primeira equação por $2$. Assim, ao somarmos as duas equações, poderemos eliminar a incógnita $y$. Fazemos:

\begin{cases}
2x & - & y & = & -2 & (\times \ 2) \\
x & + & 2y & = & -6 & \\
\end{cases}
\begin{matrix}
4x & - & 2y & = & -4 \\
x & + & 2y & = & -6 \\
\hline
5x & + & 0& =& -10
\end{matrix}

Obtendo:

$$
5x = -10\\
x = -2
$$

Substituindo  valor de $x$ na segunda equação:

$$
x + 2y = -6\\
-2 + 2y = -6\\
2y = -4\\
y = -2
$$

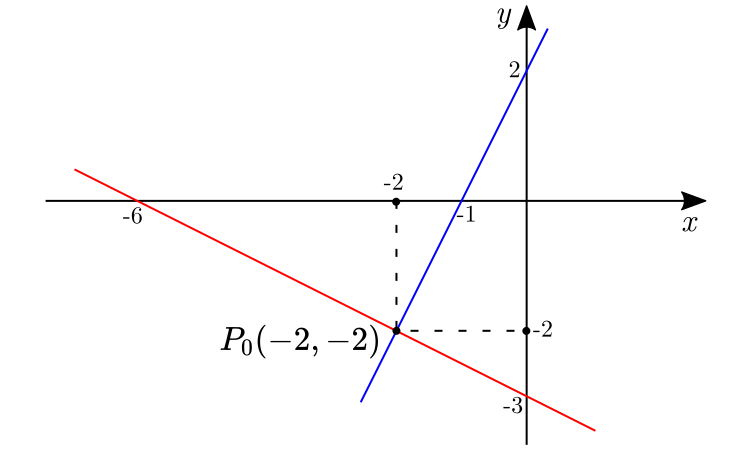
Assim, as retas $r$ e $s$ interceptam-se no ponto $P(-2,-2)$.

Graficamente:

Exemplo 4:

Determinar o ponto de de intersecção entre as retas $r$ e $s$ representadas pelas equações:

\begin{cases}
r: \quad & x & - & 2y & + & 4 & = & 0\\
s: \quad & -3x & + & 6y & + & 12 & = & 0
\end{cases}

Vamos isolar $x$ na primeira equação e substitui na segunda equação:

$$
x - 2y + 4 = 0\\
x = 2y - 4
$$

Substituindo $x$ na segunda equação:

$$
-3x + 6y + 12 = 0\\
-3(2y-4) + 6y +12 = 0\\
-6y + 12 + 6y +12 = 0\\
-6y + 6y = -24\\
0 = -24 \quad (?)
$$

A solução deste sistema mostra que as equações são independentes e que o sistema linear é impossível. Ou seja, não existe um ponto em comum porque as retas são paralelas.

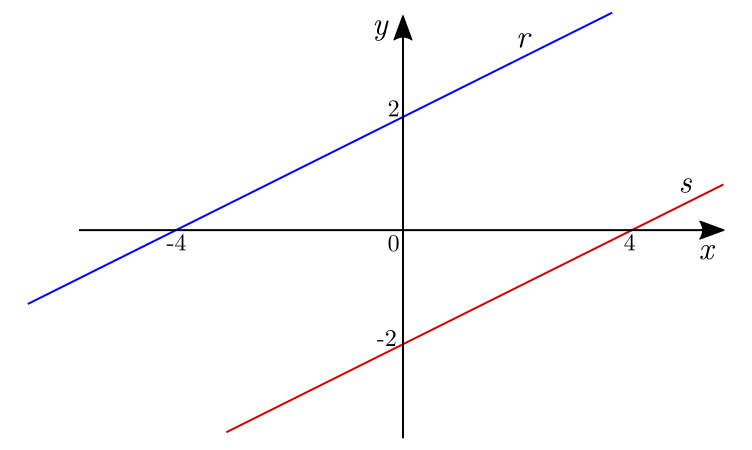
Graficamente, temos:

Download:

Você pode fazer o download deste artigo em PDF através do Google Drive:

Links para este artigo:

• https://bit.ly/interseccao-retas
  
• https://www.obaricentrodamente.com/2022/12/como-determinar-a-inteseccao-de-duas-retas.html

Veja mais:

• Retas perpendiculares
  
• Distância de um ponto a uma reta
  
• Como obter a equação reduzida da reta