Existem 4 modos para determinação de planos:
- Por três pontos não colineares
- Por uma reta e um ponto não pertencente à reta
- Por duas retas concorrentes
- Por duas retas paralelas distintas
1º Modo: Utilizando o axioma da determinação
Este primeiro modo é um postulado baseado no axioma da determinação, onde:
a) Dois pontos distintos determinam uma única reta que passa por elas:
$$\overleftrightarrow{AB\ }
$$
b) Três pontos não colineares determinam um único plano que passa por eles:
$$\alpha = (A,B,P)
$$
2º Modo: Utilizando uma reta e um ponto
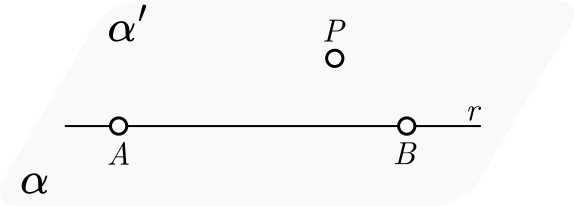
Se existir uma reta $r$ e um ponto $P$ não pertencente à $r$, então eles determinam um único plano que os contém.
Por hipótese, temos que o ponto $P$ não pertence à reta $r$:
$$P \notin r
$$
A tese que queremos demonstrar é que existe um plano $\alpha$ de modo que o ponto $P$ pertence ao plano $\alpha$ e que a reta $r$ está contida em $\alpha$:
$$\exists \ \alpha \ | \ P \in \alpha \quad \text{e} \quad r \subset \alpha
$$
Como este é um problema de existência e unicidade, vamos dividir a demonstração em duas partes:
1ª Parte: Existência
Dados um ponto $P$ e uma reta $r$, tomamos dois pontos $A$ e $B$ distintos pertencentes a $r$.
Se os pontos $A$, $B$ e $P$ não forem colineares $(A,B \in r \quad \text{e} \quad P \notin r)$, então esses pontos determinam um plano $\alpha$.
Como os pontos $A$, $B$ e $P$ determinam o plano $\alpha$, logo, o ponto $P$ pertence a esse plano:
$$\alpha = (A, B, P) \Longrightarrow P \in \alpha
$$
Por outro lado, como os pontos $A$, $B$ e $P$ determinam o plano $\alpha$, e sendo os pontos $A$ e $B$ distintos, então $A$ e $B$ pertencem à reta $r$. Logo, a reta $r$ está contida no plano $\alpha$:
$$
\left.\begin{matrix}
\alpha = (A,B,P) \\
A \neq B; \ B \in r\
\end{matrix}\right\}
\Longrightarrow r \subset \alpha
$$
\alpha = (r,P)
$$
\alpha = (r,P); A, B \in r \Longrightarrow \alpha = (A, B, P)
$$
\alpha^\prime=(r,P); A, B \in r \Longrightarrow \alpha^\prime=(A,B,P)
$$
\alpha = \alpha^\prime
$$
\exists \ \alpha \ | \ P \in \alpha \quad \text{e} \quad r \subset \alpha
$$
r \cap s = \{P\}
$$
\exists \ \alpha \ | \ r \subset \alpha \quad \text{e} \quad s \subset \alpha
$$
\alpha=(A,B,P); A,P\in r; A \neq P \Longrightarrow r \subset \alpha
$$
\alpha=(A,B,P); B,P\in s; B \neq P \Longrightarrow s \subset \alpha
$$
\alpha = (r,s)
$$
\alpha = (r,s); A, P \in r; B \in s \Longrightarrow \alpha=(A,B,P)
$$
\alpha^\prime = (r,s); A^\prime , P \in r; B^\prime \in s \Longrightarrow \\
\ \\
\alpha^\prime = (A^\prime, B^\prime, P)
$$
\left.\begin{matrix}
\alpha = (A,B,P) \\
A \neq B; \ B \in r\
\end{matrix}\right\}
\Longrightarrow r \subset \alpha
$$
Sendo assim, existe pelo menos o plano $\alpha$ determinado por $r$ e $P$:
$$\alpha = (r,P)
$$
2ª Parte: Unicidade
Para provarmos que o plano $\alpha$ é o único plano determinado pela reta $r$ e o ponto $P$, vamos supor a existência de dois planos, $\alpha$ e $\alpha ^\prime$, determinados por $r$ e $P$. Assim, teríamos:
a) Como o plano $\alpha$ é determinado pela reta $r$ e o ponto $P$ e $A$ e $B$ pertencem a $r$, então os pontos $A$, $B$ e $P$ determinam o plano $\alpha$:
$$\alpha = (r,P); A, B \in r \Longrightarrow \alpha = (A, B, P)
$$
b) Analogamente, como o plano $\alpha^\prime$ também seria determinado pela reta $r$ e o ponto $P$, com os pontos $A$ e $B$ pertencendo à reta $r$, então os pontos $A$, $B$ e $P$ determinam o plano $\alpha^\prime$:
$$\alpha^\prime=(r,P); A, B \in r \Longrightarrow \alpha^\prime=(A,B,P)
$$
Logo, os planos $\alpha$ e $\alpha^\prime$ são iguais:
$$\alpha = \alpha^\prime
$$
Sendo assim, não existe mais que um plano $(r,P)$, de modo que:
$$\exists \ \alpha \ | \ P \in \alpha \quad \text{e} \quad r \subset \alpha
$$
3º Modo: Utilizando duas retas concorrentes
Se duas retas forem concorrentes, então elas determinam um único plano que as contém.
Por hipótese, temos que o ponto $P$ é a intersecção entre as retas $r$ e $s$:
$$r \cap s = \{P\}
$$
A tese que queremos demonstrar é que existe um plano $\alpha$ de modo que as retas $r$ e $s$ estão contidas neste plano:
$$\exists \ \alpha \ | \ r \subset \alpha \quad \text{e} \quad s \subset \alpha
$$
Novamente, por se tratar de um problema de existência e unicidade, vamos dividir a demonstração em duas partes.
1ª Parte: Existência
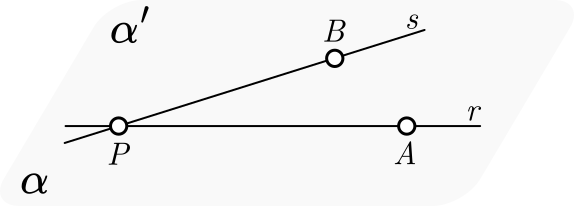
Dadas duas retas, $r$ e $s$, concorrentes em um ponto $P$, tomamos o ponto $A$ em $r$ e o ponto $B$ em $s$:
Se os pontos $A$, $B$ e $P$ não forem colineares $(A,P \in r \quad \text{e} \quad B \notin r)$, então esses pontos determinam um plano $\alpha$.
Como os pontos $A$, $B$ e $P$ determinam o plano $\alpha$, e $A$ e $P$ pertencem à reta $r$, sendo distintos, então a reta $r$ está contida no plano $\alpha$:
$$\alpha=(A,B,P); A,P\in r; A \neq P \Longrightarrow r \subset \alpha
$$
Da mesma forma, como os pontos $A$, $B$ e $P$ determinam o plano $\alpha$, e $B$ e $P$ pertencem à reta $s$, sendo distintos, então a reta $s$ está contida no plano $\alpha$:
$$\alpha=(A,B,P); B,P\in s; B \neq P \Longrightarrow s \subset \alpha
$$
Logo, existe pelo menos o plano $\alpha$ determinado pelas retas $r$ e $s$:
$$\alpha = (r,s)
$$
2ª Parte: Unicidade
Para provarmos que o plano $\alpha$ é o único plano determinado pelas retas $r$ e $s$, vamos supor a existência de dois planos, $\alpha$ e $\alpha^\prime$ determinados por $r$ e $s$. Assim, teríamos:
a) Como o plano $\alpha$ é determinado peças retas $r$ e $s$, os pontos $A$ e $P$ pertencem à reta $r$ e o ponto $B$ à reta $s$, então os pontos $A$, $B$ e $P$ determinam o plano $\alpha$:
$$\alpha = (r,s); A, P \in r; B \in s \Longrightarrow \alpha=(A,B,P)
$$
b) Analogamente, como o plano $\alpha^\prime$ também seria determinado pelas retas $r$ e $s$, com os pontos $A^\prime$ e $P$ pertencendo à reta $r$ e o ponto $B^\prime$ à reta $s$, então os pontos $A^\prime$, $B^\prime$ e $P$ determinam o plano $\alpha^\prime$:
$$\alpha^\prime = (r,s); A^\prime , P \in r; B^\prime \in s \Longrightarrow \\
\ \\
\alpha^\prime = (A^\prime, B^\prime, P)
$$
Logo, os planos $\alpha$ e $\alpha^\prime$ são iguais:
$$\alpha = \alpha^\prime
$$
Sendo assim, não existe mais que um plano $(r,s)$, de modo que:
$$\exists \ \alpha \ | \ r \subset \alpha \quad \text{e} \quad s \subset \alpha
$$
4º Modo: Utilizando duas retas paralelas
Se duas retas são paralelas e distintas entre si, então elas determinam um único plano que as contém.
Por hipótese temos que as retas $r$ e $s$ são paralelas e distintas entre si:
$$r \parallel s \quad \text{e} \quad r \neq s
$$
A tese que queremos demonstrar é que existe um plano $\alpha$ de modo que as retas $r$ e $s$ estão contidas no plano $\alpha$, sendo $r$ e $s$ distintas:
$$\exists \ \alpha \ | \ r \subset \alpha \quad \text{e} \quad s \subset s, \ r \neq s
$$
Do mesmo modo que as demonstrações anteriores, por se tratar de um problema de existência e unicidade, vamos dividir a demonstração em duas partes:
1ª Parte Existência
A existência do plano $\alpha = (r,s)$ é uma consequência da definição de retas paralelas (ou da existência dessas retas), pois duas retas são paralelas se, e somente se:
a) Ou as retas $r$ e $s$ são coincidentes:
$$r = s \Longrightarrow r \parallel s
$$
b) Ou as retas $r$ e $s$ são coplanares sem nenhum ponto comum:
$$r \subset \alpha , \ s \subset \alpha \quad \text{e} \quad r \cap s = \emptyset \Longrightarrow r \parallel s$$
Então, se as retas $r$ e $s$ forem paralelas e distintas, estas retas determinam um plano $\alpha$:
$$\exists \ \alpha \ | \ r \cap \alpha , s \cap \alpha \quad \text{e} \quad r \cap s = \emptyset
$$
Sendo assim, existe pelo menos o plano $\alpha$ determinado pelas retas paralelas $r$ e $s$:
$$\alpha = (r,s)
$$
2ª Parte: Unicidade
Para provarmos que o plano $\alpha$ é o único plano determinado pelas retas paralelas $r$ e $s$, vamos supor a existência de dois planos, $\alpha$ e $\alpha^\prime$, determinados por $r$ e $s$.
Se existirem os planos $\alpha$ e $\alpha^\prime$ passando pelas retas paralelas distintas $r$ e $s$, tomamos os pontos $A$ e $B$ distintos em $r$ e $P$ em $s$. Então, teríamos:
a) Como o plano $\alpha$ é determinado pelas retas $r$ e $s$, os pontos $A$ e $B$ são distintos e pertencem à reta $r$ e o ponto $P$ à retas $s$, então os pontos $A$, $B$ e $P$ determinam o plano $\alpha$:
$$\alpha = (r,s) ; A,B \in r, P \in s \Longrightarrow \alpha =(ABP)
$$
b) Analogamente, como o plano $\alpha^\prime$ é determinado pelas retas $r$ e $s$, os pontos $A$ e $B$ são distintos e pertencem à reta $r$ e o ponto $P$ À reta $s$, então ps pontos $A$, $B$ e $P$ determinam o plano $\alpha^\prime$:
$$\alpha^\prime = (r,s) ; A,B \in r, P \in s \Longrightarrow \alpha^\prime =(ABP)
$$
Logo, os planos $\alpha$ e $\alpha^\prime$ são iguais:
$$\alpha = \alpha^\prime
$$
Sendo assim, não existe mais que um plano $(r,s)$, de modo que:
$$\exists \ \alpha \ | \ r \cap \alpha \quad \text{e} \quad s \cap \alpha
$$
Referências:
- Fundamentos de Matemática Elementar V10 - Geometria Espacial - Osvaldo Dolce e José Nicolau Pompeo










Postar um comentário