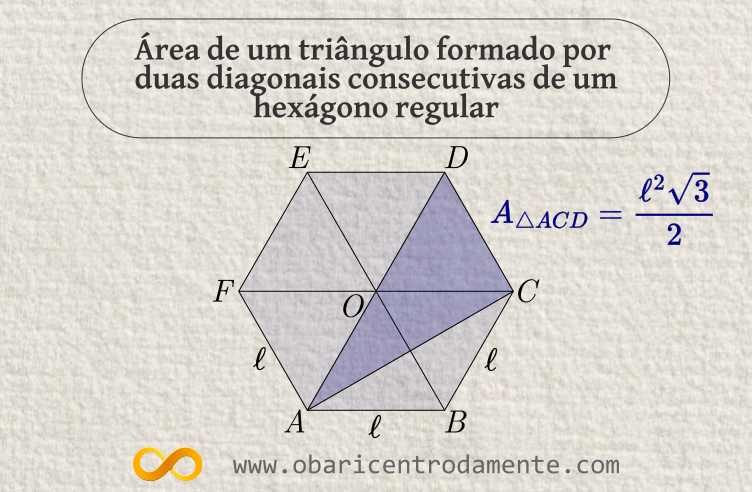
Dado um hexágono regular $ABCDEF$ de lado $\ell$, vamos encontrar uma fórmula que exprima a área de um triângulo formado quando traçamos duas diagonais consecutivas.
O hexágono regular é composto de 6 triângulos equiláteros, de modo que a área de um desses triângulos é dada por:
Primeiramente traçamos a altura $h$ do triângulo e aplicamos o teorema de Pitágoras:
$$\ell^2 = h^2 + \left(\frac{\ell}{2}\right)^2\\
\ \\
\ell^2 = h^2 + \frac{\ell^2}{4}\\
\ \\
h^2 = \ell^2 - \frac{\ell^2}{4}\\
\ \\
h^2 = \frac{3\ell^2}{4}\\
\ \\
h = \frac{\ell \sqrt{3}}{2}
$$
Aplicando na fórmula para a área de um triângulo, obtemos:
$$A = \frac{\text{base} \times \text{altura}}{2}\\
\ \\
A = \frac{\displaystyle \ell \cdot \frac{\ell \sqrt{3}}{2}}{2}\\
\ \\
A = \frac{\ell^2 \sqrt{3}}{4}
$$
Assim, a área do triângulo $\triangle CDO$ é dada por:
$$
A_{\triangle CDO} = \frac{\ell^2 \sqrt{3}}{4} \tag{1}
$$
Por construção, o quadrilátero $ABCO$ é um losango e, sendo assim, os segmentos $AC$ e $BO$ são suas diagonais, perpendiculares entre si que intersectam-se em seus pontos médios $M$. Desta forma, o triângulo $\triangle MCO$ é a metade de $\triangle BCO$ e o triângulo $\triangle AMO$ é a metade de $\triangle ABO$. Logo, suas áreas são dadas por:
$$A_{\triangle MCO} = \frac{\displaystyle \frac{\ell^2\sqrt{3}}{4}}{2} = \frac{\ell^2 \sqrt{3}}{8} \tag{2}
$$
e
$$
A_{\triangle AMO} = \frac{\displaystyle \frac{\ell^2\sqrt{3}}{4}}{2} = \frac{\ell^2 \sqrt{3}}{8} \tag{3}
$$
A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{4} + \frac{\ell^2 \sqrt{3}}{8} + \frac{\ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{2\ell^2 \sqrt{3} + \ell^2 \sqrt{3} + \ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{4 \ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{2}
$$
A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{2}\\
\ \\
A_{\triangle ACD} = \frac{2^2 \sqrt{3}}{2}\\
\ \\
A_{\triangle ACD} = 2 \sqrt{3}\ cm^2
$$
A_{\triangle AMO} = \frac{\displaystyle \frac{\ell^2\sqrt{3}}{4}}{2} = \frac{\ell^2 \sqrt{3}}{8} \tag{3}
$$
A área do triângulo $\triangle ACD$ é a soma das áreas dos três triângulos encontradas em $(1)$, $(2)$ e $(3)$:
$$A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{4} + \frac{\ell^2 \sqrt{3}}{8} + \frac{\ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{2\ell^2 \sqrt{3} + \ell^2 \sqrt{3} + \ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{4 \ell^2 \sqrt{3}}{8}\\
\ \\
A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{2}
$$
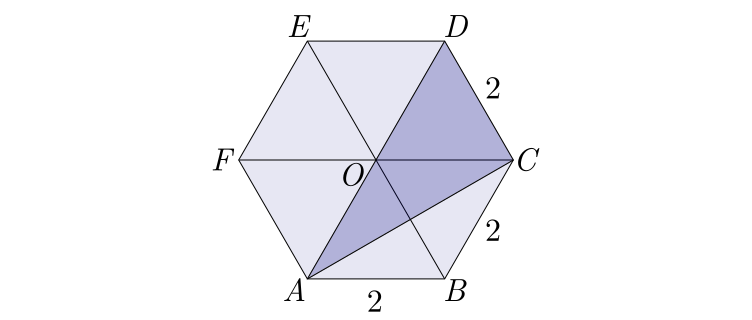
Exemplo 1:
Seja um hexágono regular $ABCDEF$ de lado igual a $2\ cm$. Calcular a área formada por duas diagonais consecutivas.
$$A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{2}\\
\ \\
A_{\triangle ACD} = \frac{2^2 \sqrt{3}}{2}\\
\ \\
A_{\triangle ACD} = 2 \sqrt{3}\ cm^2
$$
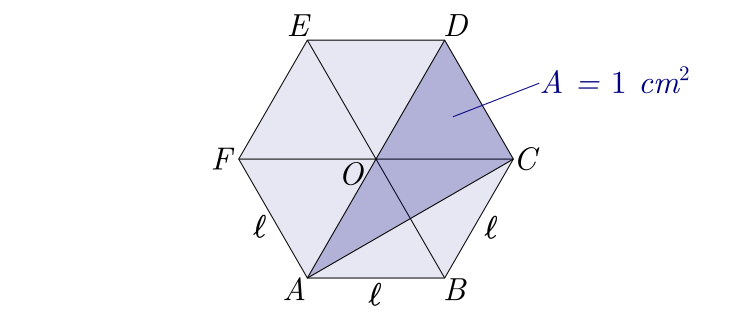
Exemplo 2:
Qual deve ser a medida do lado de um hexágono regular para que a área formada por duas diagonais consecutivas seja igual a $1\ cm^2$?
$$A_{\triangle ACD} = \frac{\ell^2 \sqrt{3}}{2}\\
\ \\
1 = \frac{\ell^2 \sqrt{3}}{2}\\
\ \\
\ell^2 \sqrt{3} = 2\\
\ \\
\ell^2 = \frac{2}{\sqrt{3}}\\
\ \\
\ell^2 = \frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\\
\ \\
\ell^2 = \frac{2\sqrt{3}}{3}\\
\ \\
\ell = \sqrt{\displaystyle \frac{2 \sqrt{3}}{3}}
$$




Postar um comentário