Dado um triângulo inscrito em uma semicircunferência, podemos utilizar derivadas para encontrar um triângulo que possua área máxima.
O problema se resume em encontrar as medidas dos catetos em função do raio $r$ da circunferência.
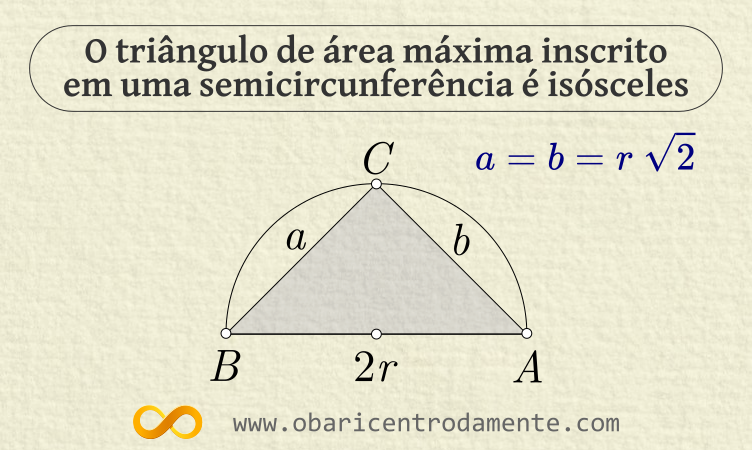
Visualmente é fácil aceitar que o triângulo de maior área é aquele cujos catetos $a$ e $b$ são iguais, ou seja, um triângulo retângulo isósceles. Mas, na Matemática, temos que demonstrar, por mais óbvio que pareça a solução.
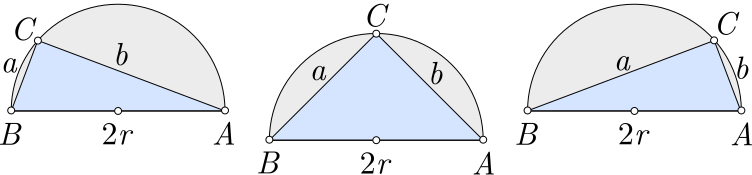
Notemos que é possível obter infinitos triângulos retângulos inscritos em uma semicircunferência de raio $r$ conforme o vértice $C$ percorre o arco $AB$ em um intervalo aberto $I=]0,2r[$, ou seja:
$$0<a<2r \quad \text{e} \quad 0<b<2r
$$
Para obtermos a área $A$ de qualquer triângulo, podemos aplicar a fórmula:
$$A = \frac{a \cdot b}{2} \tag{1}
$$
E, através do Teorema de Pitágoras, obtemos a relação:
$$a^2 + b^2 = 4r^2 \tag{2}
$$
Para encontrarmos área máxima $A$, colocamos a área em função de apenas um dos catetos ($a$ ou $b$). Vamos escolher o cateto $a$, de modo que podemos reescrever o cateto $b$ em função de $a$:
$$a^2 + b^2 = 4r^2\\
\ \\
b^2 = 4r^2 - a^2
$$
Extraindo a raiz de ambos os membros:
$$b = \sqrt{4r^2-a^2} \tag{3}
$$
Substituindo o cateto $b$ na fórmula da área, dada em $(1)$, obtemos:
$$A = \frac{1}{2}\ a\cdot b\\
\ \\
A = \frac{1}{2}\ a\cdot \sqrt{4r^2-a^2}\\
\ \\
A = \frac{1}{2}\ \sqrt{a^2(4r^2-a^2)}\\
\ \\
A = \frac{1}{2}\ \sqrt{4a^2r^2 - a^4}
$$
Agora que obtivemos uma fórmula para a área em função de um dos catetos e raio $r$, podemos aplicar a derivada:
$$A(a) = \frac{1}{2}\ \sqrt{4a^2r^2-a^4}\\
\ \\
A^\prime = \frac{1}{2}\cdot \frac{8ar^2-4a^3}{2\sqrt{4a^2r^2-a^4}}\\
\ \\
A^\prime = \frac{2ar^2-a^3}{\sqrt{4a^2r^2-a^4}}
$$
Igualamos a zero para obtermos uma equação que nos leve ao valor de máximo:
$$\frac{2ar^2-a^3}{\sqrt{4a^2r^2-a^4}} = 0
$$
Multiplicando ambos os membros da equação por $\sqrt{4a^2r^2-a^4}$, obtemos:
$$2ar^2-a^3=0\\
\ \\
a(2r^2-a^2) = 0
$$
Desta equação, temos duas respostas, mas descartamos a que $a=0$, pela obviedade. Assim:
$$2r^2-a^2=0\\
\ \\
a^2 = 2r^2
$$
Extraindo a raiz em ambos os membros:
$$a = r\sqrt{2} \tag{4}
$$
Para encontrarmos a medida do cateto $b$, substituímos o valor de $a$ obtido em $(4)$ na relação $(3)$:
$$
b = \sqrt{4r^2-a^2}\\
\ \\
b = \sqrt{4r^2-\left(r\sqrt{2}\right)}\\
\ \\
b = \sqrt{4r^2-2r^2}\\
\ \\
b = \sqrt{2r^2}
$$O que nos leva a:
$$b = \sqrt{4r^2-a^2}\\
\ \\
b = \sqrt{4r^2-\left(r\sqrt{2}\right)}\\
\ \\
b = \sqrt{4r^2-2r^2}\\
\ \\
b = \sqrt{2r^2}
$$O que nos leva a:
b = r\sqrt{2} \tag{5}
$$
Provamos, assim, que o triângulo de área máxima inscrito em uma semicircunferência de raio $r$ é aquele cujos catetos medem $a=b=r\sqrt{2}$, ou seja, isósceles.


Postar um comentário