A Geometria Plana possui muitos teorema interessantes que podem ser demonstrados por métodos analíticos seguindo algumas etapas:
- Construir uma figura que represente o problema;
- Escolher um sistema cartesiano em posição conveniente;
- Fixar as coordenadas de pontos específicos da figura impondo hipóteses;
- Fazer a demonstração.
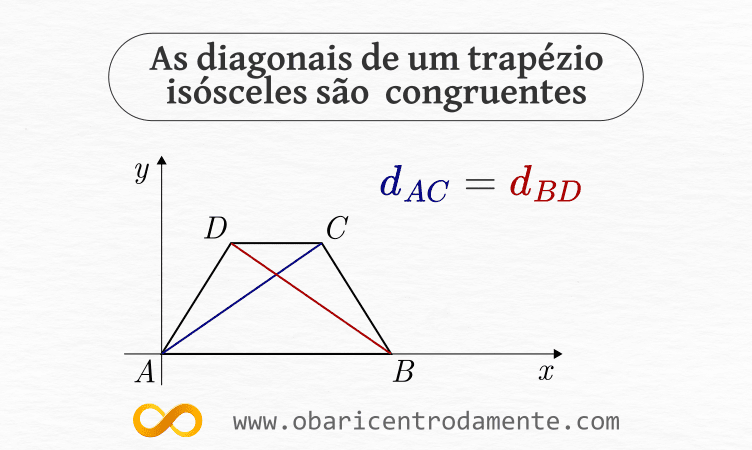
O trapézio é um quadrilátero que possui um par de lados opostos paralelos.
Um trapézio é isósceles se os dois lados oblíquos (não paralelos) forem congruentes, ou seja, possuírem o mesmo comprimento.
Podemos demonstrar que as diagonais de um trapézio isósceles são iguais utilizando a fórmula de distância entre dois pontos.
Uma das propriedades dos trapézio isósceles é que se traçarmos perpendiculares a partir dos vértices da base menor, obtemos dois triângulos congruentes.
Se o colocarmos no plano cartesiano sendo um de seus vértices a origem do sistema, podemos definir as coordenadas de um trapézio isósceles genérico:
Seja $ABCD$ um trapézio isósceles cujas coordenadas são:
$$A(0,0),\ B(a,0),\ C(b,c)\ \text{e}\ D(a-b,c)
$$
Utilizando a fórmula de distância entre dois pontos, vamos encontrar as medidas das duas diagonais.
$$d_{AC} = \sqrt{(b-0)^2 + (c-0)^2}\\
\ \\
d_{AC} = \sqrt{b^2+c^2}
$$
e
$$
d_{BD} = \sqrt{(a-b-a)^2 + (c-0)^2}\\
\ \\
d_{BD} = \sqrt{b^2+c^2}
$$
Então:
$$
AC = BD
$$
Referências:
- Fundamentos de Matemática Elementar - Geometria Analítica- Gelson Iezzi


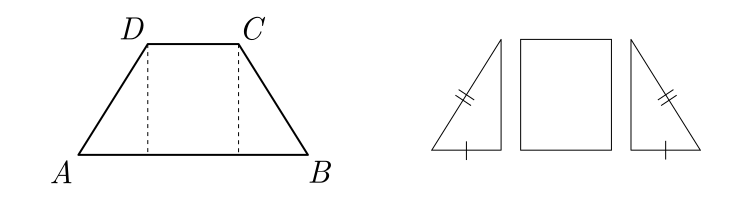

Postar um comentário