Prova do Teorema de Pitágoras utilizando a potência de um ponto

Para esta demonstração do Teorema de Pitágoras, utilizaremos as relações métricas da circunferência associadas à potência de um ponto.

Vamos primeiramente entender o que é a potência de um ponto.

Definição de potência de um ponto

Na Geometria Plana a potência de um ponto $P$ é definida como o produto de todas as suas distâncias aos pontos gerados na intersecção de uma reta que passe por $P$ e por uma circunferência dada.

Podemos ter 2 casos, sendo o ponto $P$ exterior ou interior à circunferência.

1) O ponto $P$ é exterior à circunferência

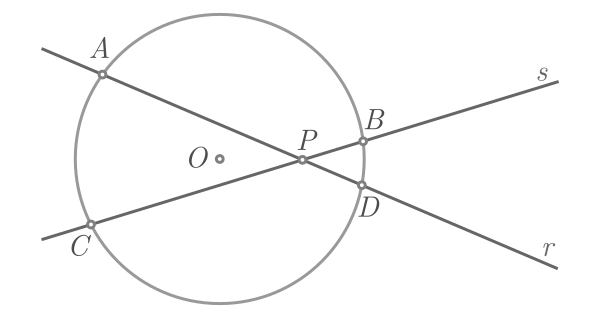
O ponto $P$ é a intersecção das retas $r$ e $s$ e está localizado no exterior da circunferência. Assim:

$$PA \cdot PB = PD \cdot PC$$

Pode ocorrer de uma das retas (ou ambas) serem tangentes à circunferência. Assim, para apenas uma das retas tangentes, temos:

$$PA \cdot PB = PC^2$$

E para ambas as retas tangentes à circunferência:

$$PA^2 = PC^2$$

2) O ponto $P$ é interior à circunferência

O ponto $P$ é a intersecção das retas $r$ e $s$ e está localizada no interior da circunferência. Assim:

$$AP \cdot PB = DP \cdot PC$$

O Teorema de Pitágoras

Vamos considerar um triângulo retângulo $ABC$:

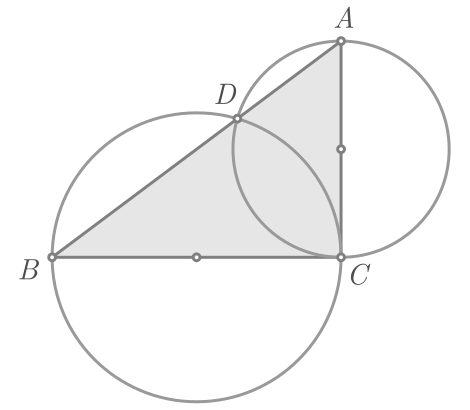
Construímos duas circunferências de diâmetros iguais aos catetos, cujos centros encontram-se sobre os pontos médios desses catetos:

O ponto $D$ é a intersecção das circunferências sobre a hipotenusa e é o pé da perpendicular baixada de $C$.

Como o segmento $CD$ é perpendicular a $AD$, logo divide o triângulo $ABC$ em outros dois triângulo retângulos: $ACD$ e $BCD$.

Como $AC$ é tangente à circunferência $BDC$, utilizamos a propriedade da potência de um ponto:

$$AC^2 = AB \cdot AD \tag{1}$$

Analogamente, como $BC$ é tangente à circunferência $ADC$, temos:

$$BC^2 = BD \cdot AB \tag{2}$$

Somando as equações $(1)$ e $(2)$, obtemos:

$$AC^2+BC^2 = AB \cdot AD + BD \cdot AB\\ \ \\ AC^2+BC^2 = AB(AD+BD)$$

Mas, como $AD+BD = AB$, temos:

$$AC^2+BC^2=AB^2$$

Demonstrando, assim, o Teorema de Pitágoras.

Links para este artigo:

• http://bit.ly/teorema-pitagoras-potencia-ponto
  
• https://www.obaricentrodamente.com/2020/12/prova-do-teorema-de-pitagoras-utilizando-a-potencia-de-um-ponto.html
  

Veja mais:

• Teorema de Pitágoras, segundo Euclides
  
• Teorema de Pitágoras baseado nas relações métricas da circunferência
  
• Teorema de Pitágoras, método de Perigal