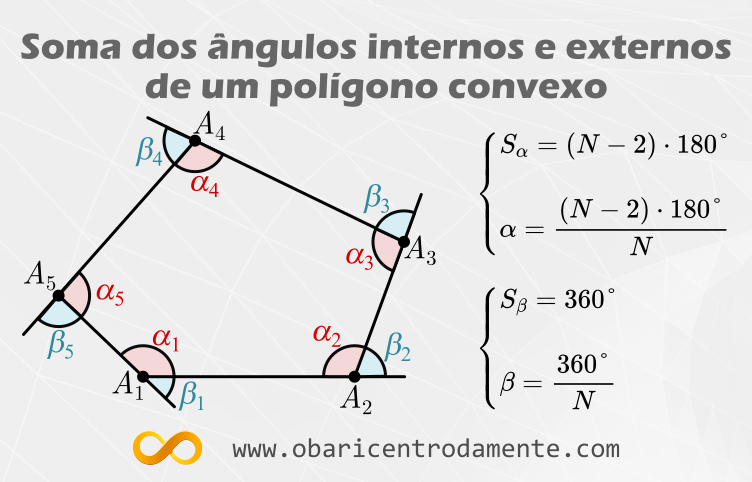
A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$.
Ângulos Internos
Definição 1:
Ângulo interno de um polígono é o ângulo formado por dois de seus lados, que seja interno ao polígono.
[Figura 1]
Teorema 1:
A soma das medidas dos ângulos internos de um polígono convexo de $N$ lados é dada pela fórmula:
\begin{equation}S_\alpha = (N-2)\cdot 180^\circ
\end{equation}
onde:
$\bullet$ $S_\alpha$ é a soma dos ângulos internos;
$\bullet$ $N$ é o número de lados do polígono.
Demonstração:
Tomando um polígono convexo, para $N>3$, podemos decompô-lo em triângulos, traçando diagonais a partir de um vértice qualquer:
[Figura 2]
Vejam que há uma relação entre o número de lados do polígono e a quantidade de triângulos em que podemos decompô-lo:
[Tabela 1]
Como soma das medidas dos ângulo internos de um polígono é igual à soma das medidas dos ângulos internos de todos os $N-2$ triângulos que o compõe, e como a soma das medidas dos ângulos internos de cada triângulo é igual a $180^\circ$, temos:
\begin{equation}S_\alpha = (N-2) \cdot 180^\circ
\end{equation}
Uma consequência direta desse resultado é a determinação do ângulo interno de um polígono regular, dado por:
\begin{equation}\alpha = \frac{(N-2)\cdot 180^\circ}{N}
\end{equation}
onde $\alpha$ é a medida de cada ângulo interno de um polígono regular de $N$ lados.
Ângulos Externos
Definição 2:
Ângulo externo de um polígono é aquele suplementar ao ângulo interno em um dado vértice, formado pelo prolongamento de um dos lados e o lado adjacente.
[Figura 3]
Teorema 2:
A soma das medidas dos ângulos externos de um polígono convexo de $N$ lados é igual a $360^\circ$:
\begin{equation}S_\beta = \beta_1, \beta_2, \beta_3, \cdots, \beta_N=360^\circ
\end{equation}
onde:
$\bullet$ $\beta_N$ é o ângulo externo do polígono;
$\bullet$ $S_\beta$ é a soma dos ângulos externos.
Demonstração:
Partimos do fato que a soma dos ângulos interno e externo é igual a um ângulo raso. Assim:
\begin{equation}\alpha + \beta = 180^\circ
\end{equation}
Então, para cada par de ângulos associados a um lado $N$ do polígono, temos:
\begin{equation}\begin{matrix}
\alpha_1 + \beta_1 = 180^\circ\\
\alpha_2 + \beta_2 = 180^\circ\\
\alpha_3 + \beta_3 = 180^\circ\\
\vdots \\
\alpha_N + \beta_N = 180^\circ\\
\end{matrix}
\end{equation}
Somando membro a membro as $N$ igualdades, obtemos:
\begin{equation}S_\alpha + S_\beta = N \cdot 180^\circ
\end{equation}
onde:
$\bullet$ $S_\alpha$ é a soma dos ângulos internos;
$\bullet$ $S_\beta$ é a soma dos ângulos externos;
$\bullet$ $N$ é o número de lados do polígono.
Manipulando a equação $(7)$, obtemos:
\begin{equation}S_\beta = N \cdot 180^\circ - S_\alpha
\end{equation}
Substituindo $S_\alpha$ dada na equação $(2)$, obtemos:
\begin{equation}\begin{matrix}
S_\beta = N\cdot 180^\circ - (N-2) \cdot 180^\circ\\
S_\beta = N\cdot 180^\circ - N\cdot 180^\circ + 360^\circ\\
S_\beta = 360^\circ
\end{matrix}
\end{equation}
Uma consequência imediata desse resultado é a determinação da medida de um ângulo externo de um polígono regular, dada por:
\begin{equation}\beta = \frac{S_\beta}{N} \qquad \text{ou} \qquad \beta = \frac{360^\circ}{N}
\end{equation}
onde $\beta$ é a medida de cada ângulo externo de um polígono regular de $N$ lados.
Exemplo 1:
Calcular a soma das medidas dos ângulos internos de um heptágono.
Temos que $N=7$, já que o polígono é um heptágono. Assim:
\begin{matrix}S_\alpha=(N-2)\cdot 180^\circ \\
S_\alpha= (7-2)\cdot 180^\circ\\
S_\alpha= 5\cdot 180^\circ\\
S_\alpha = 900^\circ
\end{matrix}
Desse modo, a soma dos ângulos internos de um heptágono vale $900^\circ$.
Exemplo 2:
Calcular a soma das medidas dos ângulos internos de um eneágono regular e determinar a medida de cada ângulo externo.
Temos que $N=9$. Fazemos:
\begin{matrix}S_\alpha = (N-2)\cdot 180^\circ\\
S_\alpha = (9-2) \cdot 180^\circ\\
S_\alpha = 7 \cdot 180^\circ\\
S_\alpha = 1260^\circ
\end{matrix}
Para sabermos quanto vale cada ângulo interno, dividimos a soma dos ângulos internos por $9$, obtendo $140^\circ$. Agora, para calcularmos o ângulo externo, basta fazermos:
\begin{matrix}\beta = 180^\circ - \alpha\\
\beta = 180^\circ - 140^\circ\\
\beta = 40^\circ
\end{matrix}
Exemplo 3:
Qual polígono possui a soma das medidas dos ângulos internos igual a $1800^\circ$?
Basta aplicarmos a fórmula:
\begin{matrix}
S_\alpha = (N-2) \cdot 180^\circ\\
1800^\cdot = 180^\circ \cdot N - 360^\circ\\
180^\circ \cdot N = 2160^\circ\\
N = 12
\end{matrix}
Logo, o polígono procurado é o dodecágono.
Exemplo 4:
Qual polígono regular possui a medida dos ângulos externos igual a $60^\circ$?
Aplicamos a fórmula dada em $(10)$:
$$\beta = \frac{360^\circ}{N}\\
N = \frac{360^\circ}{60}=6
$$
Logo, o polígono em questão é um hexágono.
Exemplo 5:
Qual é o polígono regular cuja medida do ângulo interno é o triplo da medida do ângulo externo?
Podemos escrever que $\alpha = 3\beta$. E agora substituirmos as equações $(3)$ e $(10)$:
$$\frac{(N-2)\cdot 180^\circ}{N} = 3\cdot \frac{360^\circ}{N}\\
180^\circ \cdot N - 360^\circ = 1080^\circ\\
180^\circ \cdot N = 1440^\circ\\
N=8
$$
Referências:
- Fundamentos de Matemática 7ª - Ismael Reis - Ed. Moderna






Ótima abordagem, o assunto foi explicado de uma maneira bastante objetiva e clara, tenho certeza que esse post irá tirar a dúvida de muitas pessoas que desejam saber o motivo da soma interna e externa dos ângulos terrem essas relações!
ResponderExcluirOlá Diego. Obrigado pelo comentário motivador. É um assunto interessante. Espero que possa ajudar aos estudantes.
ExcluirUm grande abraço!
Ajudooooooooooooo muitooooooo , Goosteei , Vleeu paarçaaa !" sz
ResponderExcluirÓtima postagem, Parabéns !!!
ResponderExcluirSó deixando uma correção. No Teorema 2 está:
"Teorema 2: A soma das medidas dos ângulos externos de um polígono convexo de N lados é igual a 180∘:".
No final é 360º, mas dá pra notar que é um erro de digitação pois abaixo disso está 360º.
Obrigado amigo pela leitura atenta. Já está corrigido.
ExcluirUm abraço.
um polígono de cinco lados possui cinco ângulos externos ?E vredadeirp ou falso? me ajuda por favor !
ResponderExcluirSim Leticia. Veja a figura 3.
ExcluirMuito bom , muito boa a abordagem e as explicações estão muito claras
ResponderExcluirQual é a soma dos ângulos internos de um dodecágono
ResponderExcluirUm dodecágono é o polígono que possui 12 lados. Assim, utilizamos a fórmula:
Excluir$$S_{\alpha} = (N-2)\cdot 180$$
$$S_{\alpha} = (12-2)\cdot 180$$
$$S_{\alpha} = 10 \cdot 180$$
$$S_{\alpha} = 1800$$
Assim, a soma dos ângulos internos de um dodecágono é de $1800^\circ$.
Quantos lados têm um polígono convexo cuja soma dos ângulos internos é 2160
ResponderExcluirSubstituimos $2160$ na fórmula:
Excluir$$S_{\alpha} = (N-2)\cdot 180$$
$$2160 = (N-2) \cdot 180$$
$$\frac{2160}{180} = N-2$$
$$12 = N-2$$
$$N=14$$
Assim, o polígono cuja soma dos ângulos internos é de $2160$, possui $14$ lados.
Muito obrigado seu site e um dos melhores Valeu!!!
ResponderExcluirQual a soma dos angulo externos de 14 ??
ResponderExcluir