Integral de $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$

Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica.

Seja a integral:
\begin{equation*}
\int \frac{\sqrt{16-x^2}}{4x^2}dx = I
\end{equation*}

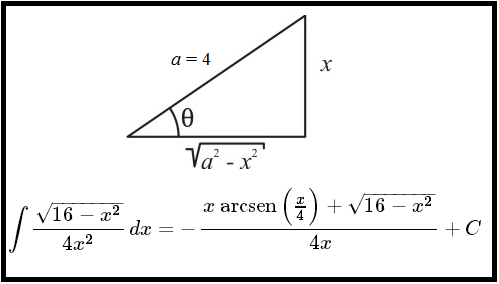
Vejam o artigo sobre o método da substituição trigonométrica para resolução de certas integrais. Com o auxílio visual, analisemos o triângulo retângulo da figura acima.

Temos que $\displaystyle \text{sen}(\theta) = \frac{x}{4} \Rightarrow x=4 \text{sen}(\theta)$ e então $dx=4\cos (\theta) d \theta$. E ainda temos que $\displaystyle \sqrt{16-x^2} = 4 \cos (\theta)$.

Assim, a integral fica:
\begin{matrix}
I = \frac{1}{4} \int \frac{4\cos (\theta)}{16 \text{sen}^2 (\theta)}\cdot 4\cos (\theta) d \theta\\
I= \frac{1}{4} \int \frac{16 \cos^2 (\theta)}{16 \text{sen}^2 (\theta)}d \theta\\
I= \frac{1}{4} \int \text{cotg}^2 (\theta) d \theta
\end{matrix}

Da identidade trigonométrica $1+\text{cotg}^2(x)=\text{cossec}^2(x)$, temos que:

\begin{equation*}
I=\frac{1}{4} \int \left( \text{cossec}^2 (\theta)-1 \right) d \theta
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I=\frac{1}{4} \int \text{cossec}^2 (\theta) d\theta - \frac{1}{4} \int 1 d\theta
\end{equation*}
A integral de $\text{cossec}^2 (\theta)$ é $-\text{cotg}(\theta)+C$. Assim:
\begin{equation*}
I=-\frac{1}{4} \cdot \text{cotg} (\theta) - \frac{1}{4} \cdot \theta + C = -\frac{1}{4}\left(\theta + \text{cotg}(\theta)\right) + C
\end{equation*}
Mas $\displaystyle \theta = \text{arcsen}\left(\frac{x}{4} \right)$ e $\displaystyle \text{cotg}(\theta) = \frac{\sqrt{16-x^2}}{x}$. Assim:
\begin{matrix}
I=-\frac{1}{4}\left( \text{arcsen}\left(\frac{x}{4}\right) + \frac{\sqrt{16-x^2}}{x}\right)+C\\
I=\int \frac{\sqrt{16-x^2}}{4x^2}dx=-\frac{x\ \text{arcsen}\left(\frac{x}{4}\right) + \sqrt{16-x^2}}{4x}+C
\end{matrix}

---

Veja mais:

Integração por Substituição Trigonométrica
Integração por Frações Parciais - Fatores Lineares
Integração por Frações Parciais - Fatores Quadráticos Irredutíveis

---