Resolução da integral $\displaystyle \int e^x \text{sen} (x) dx$

Lembra daquelas tabelas de integrais? Quando estudamos em nossa graduação, muitas vezes somente consultamos as tabelas e tomamos o resultado. Mas como esses resultados foram obtidos?

Este artigo faz parte de uma série de resoluções de integrais que venho fazendo para demonstrar os resultados que encontramos nessas tabelas.

Primeiramente a integral é resolvida passo-a-passo e em seguida é aplicada em exemplos. Para cada integral, utiliza-se técnicas específicas para sua resolução, que pode ser por substituição, por partes, por frações parciais ou substituição trigonométrica.

Nesta postagem, vamos demonstrar que:

\begin{equation*}
\int e^x \ \text{sen}(x)\ dx = \frac{1}{2}\ e^x \big( \text{sen}(x) - \cos(x)\big) + C
\end{equation*}

Seja a integral:

\begin{equation*}
I = \int e^x \ \text{sen}(x)\ dx
\end{equation*}

Para resolver esta integral, utilizaremos o método de integração por partes duas vezes consecutivas. Lembrando que:

\begin{equation*}
\int u\ dv = uv - \int v\ du \tag{1}
\end{equation*}

Fazemos: $u=\text{sen}(x)$, assim $du=\cos(x)\ dx$. E fazemos $dv=e^x\ dx$, assim $v = e^x$. Aplicando estes valores na fórmula $(1)$, obtemos:

\begin{equation*}
I = \text{sen}(x)\ e^x - \int e^x \ \cos(x)\ dx
\end{equation*}

Para o integrando $e^x\ \cos(x)$, precisamos utilizar novamente o método de integração por partes. Fazemos $u=\cos(x)$, assim $du = -\text{sen}(x)\ dx$. E fazemos $dv=e^x\ dx$, assim $v=e^x$:

\begin{equation*}
I = \text{sen}(x)\ e^x -  \cos(x)\ e^x - \int e^x \ \text{sen}(x)\ dx
\end{equation*}

Vejam que a integral que apareceu acima é a mesma integral original, que representamos por $I$. Assim, fazemos:

\begin{equation*}
I = \text{sen}(x)\ e^x - \cos(x)\ e^x - I + C\\
\ \\
2I = \text{sen}(x)\ e^x - \cos(x)\ e^x + C\\
\ \\
I = \frac{1}{2}\ e^x \big( \text{sen}(x) - \cos(x) \big) + C
\end{equation*}

Veremos agora dois exemplos aplicando a integral.

Exemplo 1:

Vamos calcular a área sob a curva $f(x) = e^x \ \text{sen}(x)$ compreendida no intervalo $[0, \pi]$.

Para calcularmos a área desejada, utilizaremos o conceito de integral definida, com limite inferior igual a $0$ e limite superior igual a $\pi$:

\begin{equation*}
A = \int_0^{\pi} e^x \ \text{sen}(x)\ dx
\end{equation*}

Utilizando o resultado que obtivemos logo acima:

\begin{equation*}
A = \left[ \frac{1}{2}\ e^x \ \big( \text{sen}(x) - \cos(x) \big) \right]_0^{\pi}\\
\ \\
A = \left[ \frac{1}{2}\ e^{\pi}\big( \text{sen}(\pi) - \cos(\pi) \big) \right] - \left[ \frac{1}{2}\ e^0 \big( \text{sen}(0) - \cos(0) \big) \right]\\
\ \\
A = \frac{1}{2}\ e^{\pi} (0+1) - \frac{1}{2} (0-1)\\
\ \\
A = \frac{1}{2}\ e^{\pi} + \frac{1}{2}\\
\ \\
A \approx 12,070
\end{equation*}

Assim, a área sombreada no gráfico, compreendida entres os pontos $x=0$ e $x=\pi$ vale aproximadamente $12,070$ unidades de área.

Exemplo 2:

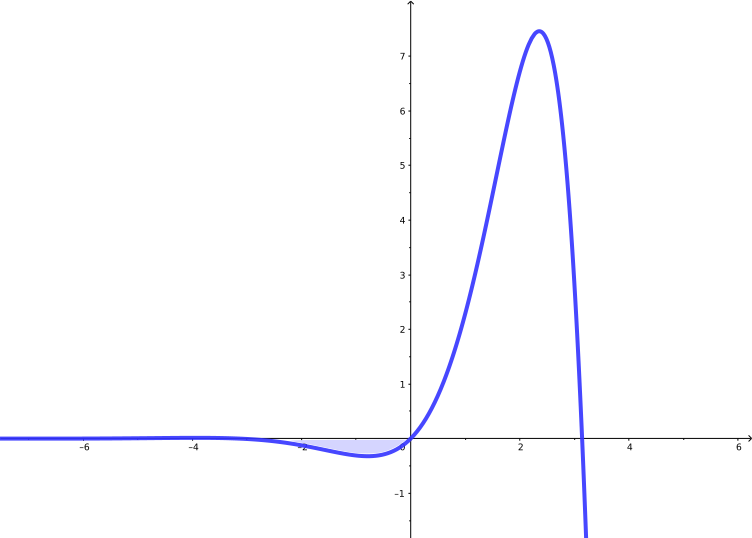
Vamos calcular a área sobre a curva $f(x) = e^x \ \text{sen}(x)$ compreendida no intervalo $[-\pi,0]$.

\begin{equation*}
A = \int_{-\pi}^0 e^x \ \text{sen}(x)\ dx\\
\ \\
A = \left[ \frac{1}{2}\ e^x \big(\text{sen}(x) - \cos(x) \big) \right]_{-\pi}^0\\
\ \\
A = \left[ \frac{1}{2}\ e^0 \big( \text{sen}(0) - \cos(0)\big) \right] - \left[ \frac{1}{2} \ e^{-\pi} \big( \text{sen}(-\pi)-\cos(-\pi)\big) \right]\\
\ \\
A = \frac{1}{2} (0-1) - \frac{1}{2e^{\pi}}(0+1)\\
\ \\
A = -\frac{1}{2} - \frac{1}{2e^{\pi}}\\
\ \\
A \approx -0,5216
\end{equation*}

Não existe área negativa. O significado disso é que a área que calculamos encontra-se sob o eixo dos $x$, como podemos observar na imagem acima.

Sendo assim, a área sombreada vale aproximadamente $0,5216$ unidades de área.

Links para este artigo:

• http://bit.ly/int-ex-senx
• https://www.obaricentrodamente.com/2019/02/resolucao-da-integral-int-ex-sen-x-dx.html

Veja mais:

• Método de integração por partes
• Resolução da integral $\ln(ax)dx$
• Cálculo da área dentre duas curvas