Neste artigo veremos como calcular a área definida por duas curvas utilizando o cálculo integral. Será necessário um conhecimento prévio sobre integrais definidas para que se possa aplicá-las de forma mais natural possível.
Vamos supor duas curvas $y=f(x)$ e $y=g(x)$ em um sistema de eixos ortogonais, cuja intersecção entre estas curvas se dê nos pontos $x=a$ e $x=b$, onde a curva $y=f(x)$ esteja acima da curva $y=g(x)$ no intervalo $[a,b]$. O que queremos é encontrar uma integral que possa representar a área definida entre estas curvas. Um meio de pensarmos é adotar retângulos verticais de larguras infinitesimais:
Os comprimentos dos retângulos são variáveis a cada ponto $x$ e pode ser representado por $f(x)-g(x)$, que é a distância da curva inferior à curva superior. A largura dos retângulos são infinitesimais e representadas por $dx$. Desse modo, o elemento de área é dado por:
dA = \big[ f(x) - g(x) \big]\ dx
\end{equation*}
A área total da região será dada pela soma das áreas de todos os retângulos de larguras infinitesimais no intervalo $[a,b]$:
A = \int dA\\
\end{equation*}
\begin{equation*}
A = \int_a^b \big[ f(x) - g(x) \big]\ dx \tag{1}
\end{equation*}
Integramos do limite inferior $a$ ao limite superior $b$, de modo que o incremento (ou diferencial) $dx$ seja positivo. Devemos assinalar também que $a$ e $b$ são os valores de $x$ para os quais as duas funções têm o mesmo valor $y$, ou seja, são as soluções da equação $f(x)=g(x)$.
O ideal é a que a fórmula $(1)$ seja construída a cada problema para que não fique algo mecânico e que assim possamos dominar o método. Muitas vezes fica mais fácil obter a fórmula para a área se pensarmos geometricamente, fazendo um esboço. Em alguns casos talvez seja mais conveniente escolher retângulos horizontais, de modo que a largura infinitesimal seja $dy$ e a área total será em função de $y$.
Passo-a-passo para calcular a área entre duas curvas:
Passo 1: Esboce a região cuja área deseja determinar. Anote as equações de cada curva os pontos de intersecção entre elas.
Passo 2: Analise se é mais conveniente utilizar retângulos verticais de largura $dx$ ou horizontais de largura $dy$ e desenhe-o no esboço.
Passo 3: Observe o esboço e use as equações das curvas para determinar a área $dA$ do retângulo de largura infinitesimal como um produto do comprimento pela base. Expresse $dA$ em termos da variável ($x$ ou $y$), dependendo da orientação escolhida.
Passo 4: Integre $dA$ entre os limites apropriados, sendo estes observados no esboço.
Exemplo 1:
Sejam as curvas $f(x) = 4$ e $g(x)=x^2$. Determinar a área entre as curvas.
A curva $y=x^2$ é uma parábola cuja concavidade voltada para cima e a curva $y=4$ é uma reta horizontal, que corta o eixo dos $y$ no ponto $4$. Os limites de integração serão os que satisfazem a equação $x^2=4$, ou seja, os pontos $x=-2$ e $x=2$. Vamos esboçar as curvas, anotando as funções, os elementos de área e os limites.

Usando retângulos verticais:
Se usarmos retângulos verticais, o comprimento será $f(x)-g(x) = 4-x^2$ e sua largura $dx$. Assim, sua área será $dA = (4-x^2)\ dx$. A área total da região é dada pela integral:
\begin{equation*}A = \int_{-2}^{2} \big( 4-x^2 \big)\ dx\\
\ \\
A = \left[4x - \frac{1}{3}x^3 \right]_{-2}^{2}\\
\ \\
A = \left(8-\frac{8}{3}\right) - \left(-8+\frac{8}{3}\right)\\
\ \\
A = \frac{32}{3}
\end{equation*}
Sempre que possível, utilizamos a simetria, a fim de simplificar os cálculo. Neste caso, a simetria proporcionada pelo eixo da parábola sugere que integremos apenas de $x=0$ a $x=2$, encontrando apenas a metade da direta. Depois, multiplicamos por $2$ para obter a área total.
\begin{equation*}A = 2\int _0^2 \big(4-x^2 \big)\ dx\\
\ \\
A = 2\left[4x-\frac{1}{3}x^3\right]_0^2\\
\ \\
A = 2\left(8-\frac{8}{3}\right)\\
\ \\
A = \frac{32}{3}
\end{equation*}
Usando retângulos horizontais:
Se usarmos retângulos horizontais, o comprimento será o valor de $x$ na extremidade direita menos o valor de $x$ na extremidade esquerda, o que equivale a $\displaystyle \sqrt{y}-\left(-\sqrt{y}\right)$ e assim, a área será dada por $\displaystyle dA=\left[\sqrt{y} - \left(-\sqrt{y}\right)\right]\ dy = 2\sqrt{y}\ dy$ e a área total será:
\begin{equation*}A = \int_0^4 2\sqrt{y}\ dy\\
\ \\
A = \left[ \frac{4}{3} y^{3/2} \right]_0^4\\
\ \\
A = \frac{32}{3}
\end{equation*}
A resposta é a mesma, o que não surpreende, mas conforta.
Exemplo 2:
Vamos calcular a área entre as curvas $f(x)=3-x^2$ e $g(x)=x+1$. Os limites de integração são dados pela intersecção das curvas, que são soluções da equação $f(x)=g(x)$. Então fazemos:
\begin{equation*}3-x^2 = x+1\\
\ \\
x^2+x-2=0\\
\ \\
x = \frac{-1 \pm \sqrt{1+8}}{2}\\
\ \\
x = \frac{-1 \pm 3}{2}\\
\ \\
x_1 = -2\\
\ \\
x_2 = 1
\end{equation*}
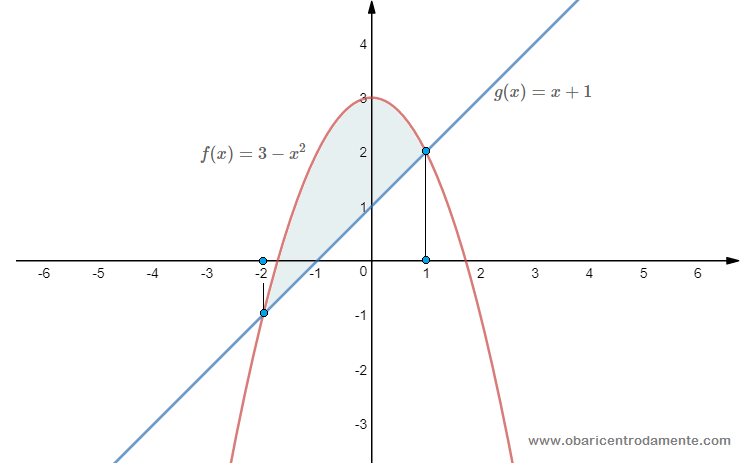
Utilizando retângulos verticais, o comprimento será $f(x)-g(x) = 3-x^2-x-1$ e sua largura é $dx$. Assim, a área deste retângulo será $dA = 2-x-x^2$, e a área total da região é dada pela integral:
\begin{equation*}A = \int _{-2}^1 \big(2-x-x^2 \big)\ dx\\
\ \\
A = \int_{-2}^1 \left[ 2x - \frac{x^2}{2} - \frac{x^3}{3} \right]_{-2}^1\\
\ \\
A = \left(2-\frac{1}{2}-\frac{1}{3}\right) - \left(-4-2+\frac{8}{3}\right)\\
\ \\
A = \frac{7}{6} + \frac{10}{3}\\
\ \\
A = \frac{27}{6}
\end{equation*}
Exemplo 3:
Vamos calcular a a área entre as curvas $f(x)=x^2+2$ e $g(x)=4-x^2$. Os limites de integração são os pontos das intersecções entre as curvas, que são as soluções da equação $f(x)=g(x)$:
\begin{equation*}x^2+2=4-x^2\\
\ \\
2x^2 = 2\\
\ \\
x^2 = 1\\
\ \\
x = \pm 1
\end{equation*}

Utilizando retângulos verticais, cujos comprimentos são dados por $g(x)-f(x)=(4-x^2)-(x^2+2)$, as áreas desses retângulos são iguais a $dA = 2-2x^2\ dx$ e a área total da região é dada pela integral:
\begin{equation*}A = \int_{-1}^1 \left( 2 -2x^2 \right)\ dx\\
\ \\
A = \left[ 2x - \frac{2}{3}x^3 \right]_{-1}^1\\
\ \\
A = \left(2-\frac{2}{3}\right) - \left(-2+\frac{2}{3}\right)\\
\ \\
A = 2-\frac{2}{3}+2-\frac{2}{3}\\
\ \\
A = \frac{8}{3}
\end{equation*}
Se usarmos a simetria das parábolas, temos:
\begin{equation*}A = 2\int_0^1 \big( 2-2x^2 \big)\ dx\\
\ \\
A = 2 \int \left[ 2x-\frac{2}{3}x^3\right]_0^1\\
\ \\
A = 2\left(2-\frac{2}{3}\right)\\
\ \\
A = \frac{8}{3}
\end{equation*}
Exemplo 4:
Vamos calcular a área entre as curvas $f(x)=\text{sen}(x)$ e $g(x)=-\text{sen}(x)$ nos intervalos de $0$ a $\pi$.

Vamos utilizar retângulos verticais com comprimentos iguais a $f(x)-g(x)=\text{sen}(x)+\text{sen}(x)$ e largura $dx$. A área desses retângulos é dada por $dA = 2\ \text{sen}(x)\ dx$ e a área total da região será dada pela integral:
\begin{equation*}A = \int_0^{\pi} 2\ \text{sen}(x)\ dx\\
\ \\
A = 2\int_0^{\pi} \text{sen}(x)\ dx\\
\ \\
A = 2\bigg[ \cos(x) \bigg]_0^{\pi}\\
\ \\
A = (-2\ \cos(\pi)) - (-2\ \cos(0))\\
\ \\
A = 2+2 = 4
\end{equation*}
Exemplo 5:
Vamos calcular a área entre as curvas $\displaystyle f(x)=-\frac{x^2}{2}-1$ e $g(x) = x^2-4x-1$. Os limites de integração são as soluções da equação $f(x)=g(x)$:
\begin{equation*}-\frac{x^2}{2}-1 = x^2-4x-1\\
\ \\
x^2+\frac{x^2}{2}-4x-1+1=0\\
\ \\
\frac{3}{2}x^2-4x=0\\
\ \\
x\left(\frac{3}{2}x-4\right)=0\\
\ \\
x_1=0\\
\ \\
x_2=\frac{8}{3}
\end{equation*}

Utilizando retângulos verticais, cujos comprimentos são dados por $\displaystyle f(x)-g(x)=-\frac{x^2}{2}-1+x^2+4x+1$ e largura$dx$, as áreas desses retângulos serão dadas por $\displaystyle dA=\left(-\frac{3}{2}x^2+4x\right)\ dx$. A área total da região é dada pela integral:
\begin{equation*}A = \int_0^{8/3} \left(-\frac{3}{2}x^2-4x\right)\ dx\\
\ \\
A = \left[ -\frac{x^3}{2} + 2x^2 \right]_0^{8/3}\\
\ \\
A = -\frac{\big(8/3\big)^3}{2} + 2\big(8/3\big)^2\\
\ \\
A = -\frac{512}{54} + \frac{128}{9}\\
\ \\
A = \frac{128}{27} \approx 4,74
\end{equation*}
Widget
O professor Edigley, em seu Blog do Professor Edigley Alexandre, disponibiliza Widget muito bacana que ele criou utilizando a plataforma do Wolfram Alpha para calcular a área entre duas curvas. Basta inserir as funções e os limites de integração. Veja um exemplo:

Além desse, Edigley fez muitos outros widgets fantásticos. Veja alguns deles:
- Calculador para sistemas lineares com até 4 equações
- Calculador para equações polinomiais de 1º grau
- Calculador trigonométrica
- Calculador para o quociente entre dois polinômios
- Volume de sólidos de revolução
- Área entre duas curvas
- Derivadas parciais
- Integrais duplas e triplas
E muito mais!
No artigo 5 passos para criar um widget, o professor Edigley ensina como criar widgets. Confiram!
Referências:
- Cálculo com Geometria Analítica V1 - Simmons
- Notas de aula



Kleber,
ResponderExcluirÀs vezes, paro e penso: nossa! Quantas oportunidades fantásticas temos hoje para estudar.
Na minha época na faculdade, a internet não era forte, os softwares não eram acessíveis.
Fico imaginando as aulas de hoje na faculdade usando o GeoGebra e todas as ferramentas que possibilitam uma melhor compreensão dos conteúdos. Nossa!
Penei muito para entender rabiscos mal feitos no quadro e explicações mais abstratas do que as obras de um pintor.
Lembro bem da primeira aula quando o professor mostrou como calcular áreas entre duas curvas e mais tarde volume. Sofri meu amigo. O uso correto desses softwares teria me salvado.
Parabéns pela ótima exposição e organização desse material. É uma ótima fonte de estudo.
Abraço!
Olá Edigley, bom receber seu comentário.
ExcluirEu entendo você perfeitamente. Quando me graduei também era assim: recursos parcos, entre softwares e blogs. Eu usava o Maple, já achava fantástico, mas o Wolfram me parece melhor. Os apps para celular estão cada vez melhores. Acho que só não aprende quem realmente não quiser.
Obrigado por toda ajuda, meu amigo.
Um abraço.
Tem app que basta escanear a equação com a câmera e veremos a resposta no passo a passo. O aluno pode usar ele como o seu professor em casa. Infelizmente muitos usam de forma errada.
ExcluirÉ facilidade demais hoje em dia.
Parabéns, excelente didática!
ResponderExcluirObrigado, Pedro!
ExcluirGostei de seu artigo, vou usar num trabalhinho de faculdade...rsrsr só uma dica, poderia deixar uma referência BIB para colar direto no LaTeX...rsrsr
ResponderExcluirobrigado Professor, você é top
ResponderExcluirEu que agradeço pelo seu tempo em ler e comentar. Abraço!
Excluir