Neste artigo, vamos verificar se a integral da soma é a soma das integrais. Para isso, utilizaremos a identidade trigonométrica fundamental $\text{sen}^2(x)+\cos^2(x)=1$ como ponto de partida, integrando termo a termo e comparando os resultados. Uma soma de integrais poderá ser realizada, se os limites de integração forem os mesmos.

Vamos mostrar que a soma das integrais $\displaystyle \int \text{sen}(x)\ dx$ e $\displaystyle \int \cos(x)\ dx$ pode ser escrita da forma $\displaystyle \int \left(\text{sen}^2(x)+\cos^2(x)\right)dx$ e o resultado esperado é o $x$.
$$
\int \text{sen}^2(x)\ dx = \frac{x}{2}-\frac{\text{sen}(2x)}{4}
$$
e
$$
\int \cos^2(x)\ dx = \frac{x}{2} + \frac{\text{sen}(2x)}{4}
$$
Se somarmos os dois resultados, teremos:
$$S = \left(\frac{x}{2}-\frac{\text{sen}(2x)}{4}\right) + \left(\frac{x}{2} + \frac{\text{sen}(2x)}{4}\right)\\
\ \\
S = \frac{x}{2}+\frac{x}{2}\\
\ \\
S = x
$$
Que era o resultado esperado. Logo, podemos escrever:
$$\int \left(\text{sen}^2(x)+\cos^2(x)\right) dx = \int dx
$$
Verificando assim a validade da soma de integrais.
Se fizermos $x=1$ fica fácil visualizar que o resultado é $1$, pois $\text{sen}^2(1)+\cos^2(1)=1$. Por outro lado, como forma de visualizar graficamente a igualdade, podemos usar o conceito de integral definida. Tomando a gráfico da imagem acima, onde temos plotadas as curvas $f(x)=\text{sen}^2(x)$ e $g(x)=\cos^2(x)$, vamos tomar os limites de integração de $0$ a $1$.
Assim, para $f(x)=\text{sen}^2(x)$, temos
$$
\int_0^1 \text{sen}^2(x)dx
$$
Que graficamente fica:
 E para $g(x)=\cos^2(x)$, temos:
E para $g(x)=\cos^2(x)$, temos:
$$
\int_0^1 \cos^2(x)dx
$$
Que graficamente fica:

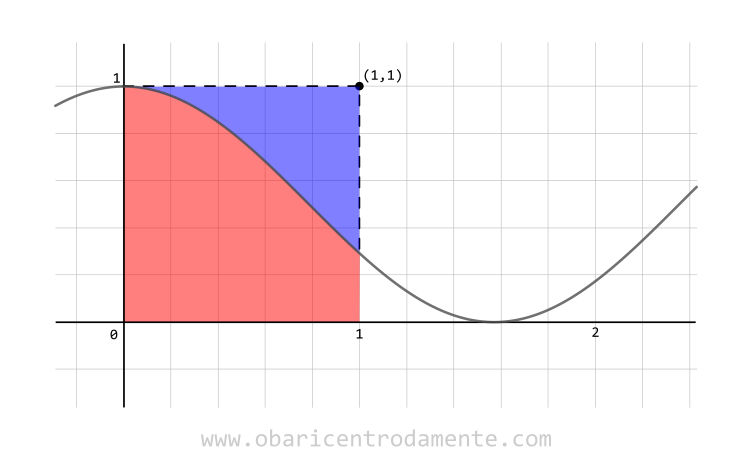
E agora, se pegarmos as áreas sob as curvas individualmente e fizermos uma manipulação em qualquer uma delas, digamos em $f(x)$, girando $90^\circ$ e depois espelhando verticalmente, obteremos um quadrado de área igual a $1$:
Este artigo foi escrito por Carlos Fernando Knauer, Graduado em Matemática.
Se fizermos $x=1$ fica fácil visualizar que o resultado é $1$, pois $\text{sen}^2(1)+\cos^2(1)=1$. Por outro lado, como forma de visualizar graficamente a igualdade, podemos usar o conceito de integral definida. Tomando a gráfico da imagem acima, onde temos plotadas as curvas $f(x)=\text{sen}^2(x)$ e $g(x)=\cos^2(x)$, vamos tomar os limites de integração de $0$ a $1$.
Assim, para $f(x)=\text{sen}^2(x)$, temos
$$
\int_0^1 \text{sen}^2(x)dx
$$
Que graficamente fica:

$$
\int_0^1 \cos^2(x)dx
$$
Que graficamente fica:

E agora, se pegarmos as áreas sob as curvas individualmente e fizermos uma manipulação em qualquer uma delas, digamos em $f(x)$, girando $90^\circ$ e depois espelhando verticalmente, obteremos um quadrado de área igual a $1$:

Este artigo foi escrito por Carlos Fernando Knauer, Graduado em Matemática.
Links para este artigo:
- http://bit.ly/soma-de-integrais
- https://www.obaricentrodamente.com/2019/10/verificacao-de-que-a-integral-da-soma-e-a-soma-das-integrais.html


Postar um comentário