Representação de expressões algébricas através de figuras planas

Desde os anos iniciais do Ensino Fundamental exploramos situações-problemas que contribuem para o desenvolvimento do pensamento algébrico, para que, depois, possamos compreender os conceitos quando iniciamos o trabalho com a Álgebra.

Uma expressão numérica é aquela que utiliza uma combinação entre números e operadores matemáticos com a finalidade de se obter um resultado, utilizando regras de prioridades em sua resolução:

$$
3 + 5 \times \left[ 1 + 2(4-1) \right] \div 2
$$

Quando incluímos letras (representando variáveis), passa-se a chamar expressões algébricas:

$$
2\cdot x^2 - 2 \cdot x + 5
$$

Esta expressão possui três termos algébricos: $2\cdot x^2$, $-2\cdot x$ e $5$.

Um termo algébrico (ou monômio) é um produto entre números, letras ou de ambos. Por exemplo:

• $5ax^2$ é um monômio, pois representa cinco vezes a quantidade $a$ multiplicada por $x^2$;
• $13$ é um monômio, pois representa uma vez a quantidade $13$;
• $x$ é um monômio, pois representa uma vez a quantidade $x$.

Podemos representar essas expressões numéricas ou algébricas em forma de figuras geométricas, sejam elas planas ou espaciais. No entanto, iremos neste artigo nos concentrar apenas em figuras planas e, sendo assim, o máximo que teremos serão monômios de grau $2$.

Essas representações estão diretamente conectadas à áreas de figuras planas sendo que as mais simples de todas são os retângulos.

Aprendemos que a área de um retângulo é dada pelo produto entre dois de seus lados adjacentes, ou o produto entre a base e a altura:

Então, a área desse retângulo é dada pela multiplicação da base pela altura, ou seja $5 \times 2$, correspondendo a $10$ unidades de área.

Por exemplo, se tivermos um retângulo genérico, cujos lados são letras (variáveis):

Para obtermos sua área, procedemos da mesma maneira, multiplicando a base pela altura, ou seja $x \times y$.

Isso significa que a área depende dos valores atribuídos aos lados do retângulo e que, quando alteramos os valores atribuídos aos lados $x$ ou $y$, obteremos uma área diferente.

Podemos fazer o processo inverso, partindo de um monômio e chegarmos à sua representação geométrica.

Vamos construir as representações de expressões algébricas através de vários exemplos, partindo de monômios simples até expressões mais complexas.

Exemplo 1:

Vamos representar geometricamente a expressão $3a$.

Como o monômio $3a$ sugere uma multiplicação de $3$ por $a$, um retângulo simples de lados $3$ e $a$ resolve o problema:

E como a área do retângulo é dada pelo produto da base pela altura, temos que a área do retângulo é dada por:

$$
A = 3a
$$

Exemplo 2:

Representar geometricamente a expressão $2x^2$.

Aqui temos $2$ que multiplica $x^2$ e podemos pensar que $x^2$ é a área de um quadrado. Assim, temos duas vezes a área de um quadrado de lado $x$:

A área da figura é dada por:

$$
A = x^2 + x^2 = 2x^2
$$

Exemplo 3:

Representar geometricamente a expressão $3ab$.

Podemos pensar que o $3$ multiplica um retângulo de lados $a$ e $b$. Assim, temos três vezes a área de um retângulo de lados $a$ e $b$:

A área da figura é dada por:

$$
A = ab + ab + ab = 3ab
$$

Exemplo 4:

Representar geometricamente a expressão $5(a+b)$.

Neste caso, temos $5$ vezes a quantidade $(a+b)$. Então, podemos pensar em um retângulo onde um de seus lados mede $5$ e o outro é a soma de dois segmentos $a$ e $b$, resultando em um segmento único de comprimento $a+b$:

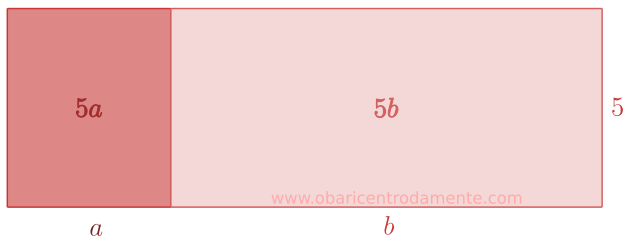
Ou ainda, podemos manipular a expressão, aplicando a propriedade distributiva, para termos uma outra visão, que no final, chega ao mesmo resultado:

$$
5(a+b)\\
\ \\
5a+5b
$$

Essa expressão sugere a soma de dois retângulos, um de lados $5$ e $a$  e outro de lados $5$ e $b$, que no fim, a representação geométrica é a mesma acima.

A área dessa figura é dada por:

$$
A = 5a+5b=5(a+b)
$$

Exemplo 5:

Representar geometricamente a expressão $x^2+3x$.

Temos uma soma entre dois monômios, onde $x^2$ representa a área de um quadrado de lado $x$ e $3x$ representa a área de um retângulo de lados $3$ e $x$.

Ou ainda, podemos manipular a expressão colocando a variável $x$ em evidência:

$$
x^2+3x\\
\ \\
x(x+3)
$$

Desta forma, temos um retângulo de lados iguais a $x$ e $(x+3)$, que por fim, remete à mesma imagem acima.

A área dessa figura é da da por:
$$
A = x^2+3x
$$

Exemplo 6:

Representar geometricamente a expressão $(a+b)^2$.

A expressão sugere um quadrado de lados $a+b$, de modo que, quando desejamos encontrar sua área, multiplicamos a base e a altura (que são iguais) obtendo a expressão original.

Esta representação é formada por quatro quadriláteros que, por sua vez, representam cada monômio do produto notável $(a+b)^2$:

$$
(a+b)^2\\
\ \\
(a+b)(a+b)\\
\ \\
a^2+ab+ab+b^2
$$

Se somarmos as áreas de cada um desses quadriláteros, obteremos uma área que representa a expressão original:

$$
A = (a+b)^2
$$

Exemplo 7:

Representar geometricamente a expressão $(a-b)^2$.

A expressão sugere a área de um quadrado cujos lados medem $a-b$. Então, fazemos um quadrado de lado igual a $a$, que é uma soma de dois segmentos, um sendo $b$ e outro $a-b$. Assim, podemos esboçar a figura:

Esta representação é formada por quatro quadriláteros que, por sua vez, representam cada monômio do produto notável $(a-b)^2$. No entanto, o único quadrilátero que representa a expressão é o quadrado em destaque com lado medindo $(a-b)$, cuja área vale $(a-b)^2$.

A área do quadrado cinza é o mesmo que o produto notável expandido:
$$
(a-b)^2 = a^2-2ab+b^2
$$
E se somarmos cada um dos quadriláteros brancos da imagem acima e subtraírmos do quadrado maior de lado igual a $a$, obteremos uma área igual à área do quadrado cinza:
$$
a^2 - {b^2 + [b(a-b)] + [b(a-b)]}\\
\ \\
a^2 - {b^2 + 2b(a-b)}\\
\ \\
a^2 - {b^2 + 2ab -2b^2}\\
\ \\
a^2 - b^2 -2ab + 2b^2\\
\ \\
a^2 -2ab + b^2
$$

Você pode criar exercícios com diversas expressões de complexidades variadas. Assim, você adquire mais habilidade, treina seu cérebro a reconhecer soluções não-triviais e aprimora seu raciocínio lógico.

Veja também:

O professor Edigley, escreveu um excelente artigo em seu blog sobre como Visualizar propriedades algébricas, contendo inclusive produtos notáveis em forma cúbica.

https://www.prof-edigleyalexandre.com/2012/09/visualizando-propriedades-algebricas.html

Links para o artigo:

• http://bit.ly/representacoes-geometricas
• https://www.obaricentrodamente.com/2020/02/representacao-de-expressoes-algebricas-atraves-de-figuras-planas.html

Veja mais:

• Como pensar geometricamente multiplicação de frações
• Aspectos geométricos para multiplicação de frações
• Fatoração de expressões algébricas