Como pensar geometricamente a multiplicação de frações

Quando temos uma multiplicação entre frações, o que fazemos para obter o produto é efetuar uma multiplicação entre os numeradores e entre os denominadores.

Por exemplo, se quisermos saber o produto entre as frações $\displaystyle \frac{3}{4}$ e $\displaystyle \frac{2}{5}$, basta multiplicarmos seus numeradores: $3 \times 2 = 6$ e seus denominadores: $4 \times 5 = 20$, assim:

\begin{equation*}
\frac{3}{4} \times \frac{2}{5} = \frac{6}{20}
\end{equation*}

Uma forma de visualizar este produto é usarmos figuras geométricas, por exemplo, quadrados subdivididos em partes iguais ao denominador, pintando ou hachurando, partes iguais ao numerador das frações em questão. A intersecção das partes pintadas será o numerador do produto e a quantidade de subdivisões será o denominador.

O que fazemos é o seguinte: tomando as frações da imagem acima, para a primeira fração $\displaystyle \frac{3}{4}$, desenhamos um quadrado e o subdividimos em partes iguais ao denominador, no caso 4 partes iguais, e pintamos partes iguais ao seu numerador, no caso 3 partes. Ou seja, pegamos 1 inteiro, dividimos em 4 partes iguais e usamos apenas 3 partes.

Para a segunda fração $\displaystyle \frac{2}{5}$, procedemos da mesma forma: subdividimo o quadrado em partes iguais ao denominador, no caso 5 partes iguais, e pintamos partes iguais ao seu numerador, no caso 2 partes. Ou seja, pegamos 1 inteiro, dividimos em 5 partes iguais e usamos apenas 2 partes.

O produto desejado se da quando sobrepomos os dois quadrados. O numerador será a intersecção das partes usadas, no caso 6, e o denominador será igual à quantidade total das subdivisões, no caso 20. Assim:

\begin{equation*}
\frac{3}{4} \times \frac{2}{5} = \frac{6}{20}
\end{equation*}

Exemplo 2:

Vamos encontrar o produto $\displaystyle \frac{1}{2} \times \frac{3}{7}$.

Começamos dividindo o primeiro quadrado em 2 partes e pintando 1 parte; e para o segundo quadrado, o dividimos em 7 partes e pintamos 3 partes. O numerador do produto é dado pela intersecção das partes usadas, no caso 3, e o denominador será a quantidade de subdivisões, no caso 14. Assim:

\begin{equation*}
\frac{1}{2} \times \frac{3}{7} = \frac{3}{14}
\end{equation*}

Exemplo 3:

Vamos encontrar o produto $\displaystyle \frac{4}{5} \times \frac{7}{8}$.

Começamos dividindo o primeiro quadrado em 5 partes e pintando 4 parte; e para o segundo quadrado, o dividimos em 8 partes e pintamos 7 partes. O numerador do produto é dado pela intersecção das partes usadas, no caso 28, e o denominador será a quantidade de subdivisões, no caso 40. Assim:

\begin{equation*}
\frac{4}{5} \times \frac{7}{8} = \frac{28}{40}
\end{equation*}

Exemplo 4:

Vamos efetuar a multiplicação $\displaystyle \frac{3}{2} \times \frac{5}{3}$.

Veste caso, temos das frações impróprias. Temos que transformá-la em uma soma de inteiros com uma fração própria.

Para a fração $\displaystyle \frac{3}{2}$, temos que:

\begin{equation*}
\frac{3}{2} = 1 + \frac{1}{2}
\end{equation*}

Para a fração $\displaystyle \frac{5}{3}$, temos que:

\begin{equation*}
\frac{5}{3} = 1 + \frac{2}{3}
\end{equation*}

A forma como devemos proceder para encontrar o produto é um pouco diferente, utilizando o mesmo princípio, mas nos lançando mão da propriedade distributiva:

O que resulta em:

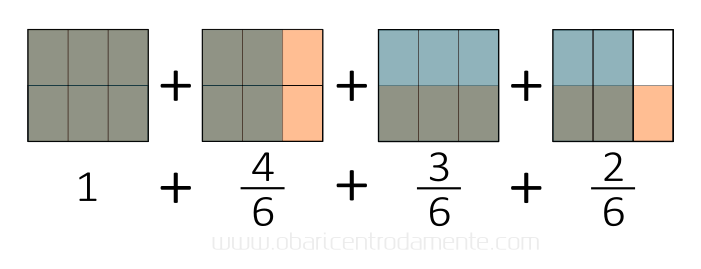
Para obter esta soma, basta tomarmos como numerador a quantidade de partes pintadas, no caso 15; e o denominador é igual à quantidade de subdivisões de cada quadrado, no caso 6. Assim:
\begin{equation*}
\frac{3}{2} \times \frac{5}{3} = \frac{15}{6}
\end{equation*}

Divisão entre frações:

Quando você faz a divisão entre duas frações, você entende o processo? Ou simplesmente obedece à máxima:

Repete a primeira fração e multiplica pelo inverso da segunda fração. Pronto! Agora resolva essas divisões sempre dessa forma e nunca errará.

No blog do Professor Alexandre tem um excelente artigo: Repete a primeira fração e multiplica pelo inverso da segunda fração. Qual a razão para essa ordem?, onde mostra didaticamente como efetuar a divisão entre frações e o por que de se fazer da forma que estamos acostumados. Recomendo a leitura imediatamente!

Links para este artigo:

• http://bit.ly/multiplicação-frações
• https://www.obaricentrodamente.com/2018/09/como-pensar-geometricamente-multiplicao-de-fracoes.html

Veja mais:

• Aspectos geométricos para multiplicação de frações
• Fração geratriz de dízima periódica
• Frações unitárias