A multiplicação é uma das quatro operações fundamentais da Matemática. A saber: adição, subtração, multiplicação e divisão.
Podemos pensar na multiplicação como uma soma de várias parcelas iguais. Se efetivamente você fizer isso não tem problema, chegará ao resultado. Funciona muito bem quando apenas pequenas quantidades são envolvidas. No entanto, conforme as quantidades aumentam, torna-se cada vez mais difícil fazer esse cálculo. E é aí que entra a multiplicação.

Para expressarmos uma multiplicação, utilizamos um símbolo para representar a operação. Esse símbolo é chamado de operador.
Hoje em dia, utilizamos alguns diferentes operadores:
- O xis: $(\times )$
- O ponto: $(\cdot)$
- O asterisco: $(∗)$
Leia o artigo: Origem dos símbolos para multiplicação
Cada termo que está sendo multiplicado é chamado de fator. O resultado da multiplicação é chamado de produto e o sinal para a multiplicação é chamado de operador. Daí o nome "operação".
O que você entende por multiplicação?
Existem significados diferentes para esta operação:
1) Adição de parcelas iguais:
Podemos pensar na multiplicação como uma adição de parcelas iguais. Por exemplo:
$$3 \times 5 = 15
$$
Neste caso, temos que $15$ é igual a $3$ vezes $5$. O fator $3$ determina o número de vezes que a parcela $5$ se repetirá, ou seja, quantas vezes será somada. Por este motivo, o primeiro fator é chamado de multiplicador, e o segundo, multiplicando.
Observe que na multiplicação acima, $5 \times 3$ também é igual a $15$. E neste caso, o fator $5$ será o multiplicador, e $3$ será o multiplicando, e indica que a parcela $5$ deve ser somada por três vezes.

2) Contagem de um arranjo em uma forma retangular
A multiplicação também pode ser pensada como o resultado de objetos arranjados em uma configuração retangular. Por exemplo, na imagem abaixo temos um total de $6$ laranjas arranjadas de tal forma que temos duas linhas e três colunas:

Observe que podemos representar a quantidade total de laranjas de duas formas: através da multiplicação $2 \times 3$ ou por $3 \times 2$.
A multiplicação $2 \times 3$ indica que a linha que contém três laranjas se repete duas vezes e, contando todas as laranjas, obtemos um total de $6$.
A multiplicação $3 \times 2$ indica que a coluna que contêm duas laranjas e repete três vezes, e, contando todas as laranjas, obtemos um total de $6$.
Com esta representação em arranjo retangular fica fácil de associar à área de um objeto qualquer. Vamos tomar um outro exemplo: considere um papel quadriculado onde cada quadrado mede $1$ centímetro de lado. Vamos pintar um total de $8$ quadrados, sendo duas linhas e quatro colunas:

Com o mesmo raciocínio do exemplo anterior, podemos obter a quantidade total fazendo $2 \times 4$ ou $4 \times 2$, obtendo em ambos os casos a quantidade de $8$.
Como cada quadrado tem lado igual a $1\ cm$, se tomarmos a multiplicação $2 \times 4$, obtemos:
$$2\ cm \times 4 \ cm = 8\ cm \times cm = 8\ cm^2
$$
É por isso que a unidade de medida de uma área está sempre elevada ao quadrado: $m^2$ ou $cm^2$, por exemplo.
3) Combinação
Quando você se prepara para sair com @s amig@s e começa a escolher sua roupa, você pensa em combinar uma calça jeans com uma camisa, ou uma blusa, pensa nas cores e coisas assim. Sem saber, você está fazendo uma análise combinatória, mas não na forma tradicional e também sem pensar em números.
Para efeito de exemplo, suponha que você tenha $2$ calças jeans e $3$ camisas. Então, você poderá combinar essas peças de roupas em $6$ maneiras diferentes. Como? Vejam só:
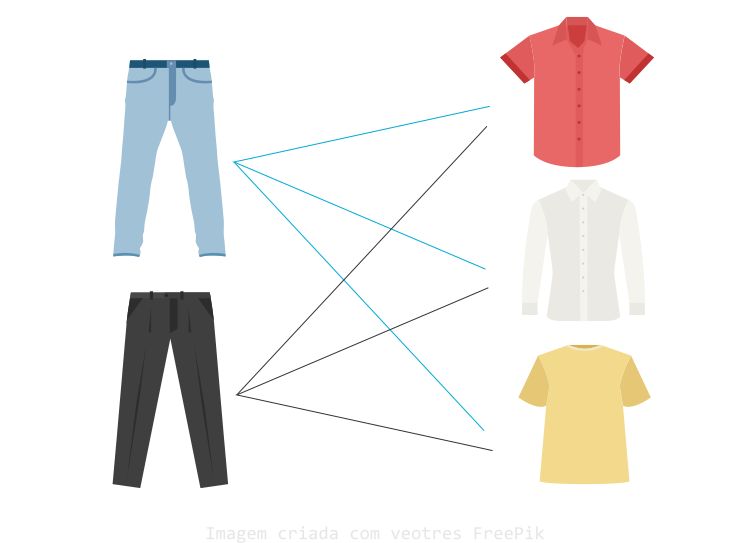
Então, quando quando tivermos grupos de objetos diferentes e tivermos que escolher apenas um objeto de cada grupo, a quantidade de possibilidades de combinações é a multiplicação das quantidades de cada grupo. No exemplo acima temos $2$ calças e $3$ camisas. Fazemos:
$$2 \times 3 = 6
$$
Assim teremos seis possibilidades.
Pensando em um exemplo mais complexo, imagine que você vá até uma lanchonete e compre um lanche onde você deva escolher apenas um item de cada ingrediente:

Assim, temos $3$ tipos de pães, $4$ tipos de molhos, $3$ tipos de salada, $5$ tipos de carnes, $3$ tipos de acompanhamento e $3$ tipos de bebida. A sua escolha será uma entre $1.620$ possibilidades:
$$3 \times 4 \times 3 \times 5 \times 3 \times 3 = 1.620
$$
4) Contexto multiplicativo
Neste caso, utilizamos a palavra "vezes" para indicar uma multiplicação. Hoje em dia ainda usamos em alguns casos, mas antigamente, antes do surgimento da simbologia matemática, os problemas eram escritos e resolvidos de forma verbal. Era chamada de Matemática Retórica.
Leia o artigo: Você sabe o que é Matemática retórica? no blog do Professor Edigley.
Vejamos alguns exemplos:
- Em uma sala de aula de uma escola de Ensino Fundamental, a quantidade de meninas é $3$ vezes a quantidade de meninos. Se a quantidade de meninos for $8$, então a quantidade de meninas será $3 \times 8 = 24$.
- $36$ é $4$ vezes maior que $9$.
- O salário de um profissional com Ensino Superior é $2$ vezes o salário de um profissional com Ensino Médio, atuando em uma mesma profissão.
Mas sempre devemos nos atentar como a palavra vezes é empregada em um problema, pois pode estar indicando uma divisão. Temos que entender que, se a palavra vezes estiver acompanhada da palavra maior, então se trata de uma multiplicação; se estiver acompanhada da palavra menor, então é uma divisão:
- O número $50$ é cinco vezes maior que $10$.
- O número $10$ é cinco vezes menor que $50$.
Referências:
- Apostila Anglo 6º Ano do Ensino Fundamental
Links para este artigo:
- https://bit.ly/conceitos-multiplicacao
- https://www.obaricentrodamente.com/2020/05/conceitos-sobre-multiplicacao.html


Postar um comentário