Neste artigo, veremos como encontrar a derivada da função inversa arco cosseno, onde:
$$\frac{d}{dx} \cos^{-1}(x) = -\frac{1}{\sqrt{1-x^2}}
$$
Para derivadas de funções inversas, uma forma de resolver é utilizar a diferenciação implícita juntamente com a regra da cadeia, porque assim não precisamos empregar outras derivadas de funções inversas no processo.
A diferenciação implícita permite encontrar a derivada de uma equação sem que esta esteja resolvida para $y$.
A função $\text{arco cosseno}$ de $x$ é a função inversa da função $\text{cos}$ de $x$ e pode ser representada como:
$$f(x)=\arccos (x) \qquad \text{ou} \qquad f(x)=\cos^{-1}(x)
$$
O que esta função quer dizer é: quais são os arcos que possuem o cosseno igual a $x$?
Dada uma função $f(x) = \cos^{-1}(x)$, fazemos:
$$\cos(y)=x \tag{1}
$$
Iniciamos derivando (implicitamente) termo a termo a equação:
$$\frac{d}{dx}\ \cos(y) = \frac{d}{dx}\ x
$$
Obtendo:
$$-\text{sen}(y)\ \frac{dy}{dx} = 1 \tag{2}
$$
A relação trigonométrica fundamental nos garante que:
$$\text{sen}^2(\theta) + \cos^2(\theta) = 1\\
\ \\
\text{sen}^2(\theta) = 1- \cos^2(\theta)\\
\ \\
\text{sen}(\theta) = \sqrt{1-\cos^2(\theta)}
$$
Fazendo $y=\theta$, substituímos $\text{sen}(y)$ na relação $(2)$, obtendo:
$$-\sqrt{1- \cos^2(y)}\ \frac{dy}{dx} = 1
$$
O que nos leva a:
$$\frac{dy}{dx} = -\frac{1}{\sqrt{1-\cos^2(y)}} \tag{3}
$$
Agora, substituímos a relação $(1)$ em $(3)$ para finalmente obter:
$$\frac{dy}{dx} = - \frac{1}{\sqrt{1-x^2}}
$$
Então, se:



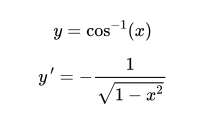
muito bom material
ResponderExcluir