Através da fórmula para o ponto médio de um segmento, conseguimos demonstrar que os pontos médios de um quadrilátero qualquer são os vértices de um paralelogramo. Nos apoiamos em uma das propriedades dos paralelogramos: as diagonais interceptam-se em seus respectivos pontos médios.
Assim, se demonstrarmos que os pontos médios das diagonais são coincidentes, provamos o teorema.
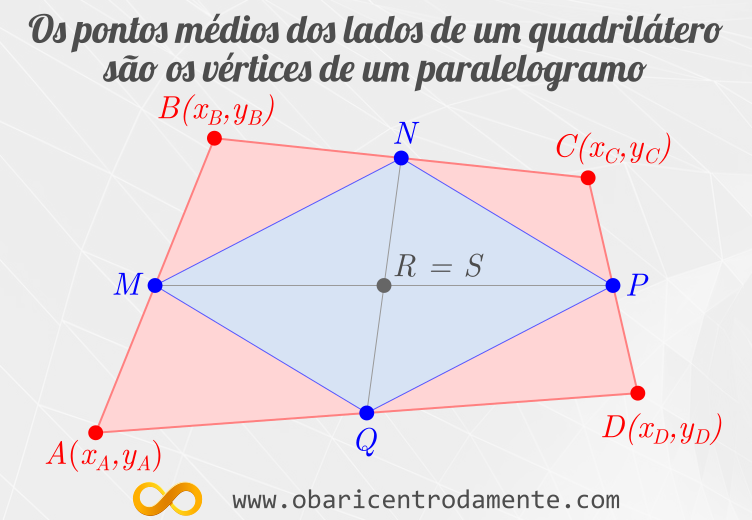
Vamos considerar o quadrilátero $ABCD$, cujas coordenadas são dadas por: $A(x_A,y_A)$, $B(x_B,y_B)$, $C(x_C,y_C)$ e $D(x_D,y_D)$.
Sejam $M$, $N$, $P$ e $Q$ os pontos médios dos lados $AB$, $BC$, $CD$ e $DA$, respectivamente. Vamos encontrar as coordenadas dos pontos médios baseados nas coordenadas dos vértices do quadrilátero. Temos que:
$$
\begin{cases}
\displaystyle M\left( \frac{x_A+x_B}{2}, \frac{y_A+y_B}{2} \right)\\
\ \\
\displaystyle N\left( \frac{x_B+x_C}{2}, \frac{y_B+y_C}{2} \right)\\
\ \\
\displaystyle P\left( \frac{x_C+x_D}{2}, \frac{y_C+y_D}{2} \right)\\
\ \\
\displaystyle Q\left( \frac{x_D+x_A}{2}, \frac{y_D+y_A}{2} \right)\\
\end{cases}
$$
R:
\begin{cases}
\displaystyle x_R = \frac{x_N+x_Q}{2}\\
\ \\
\displaystyle y_R = \frac{y_N+y_Q}{2}
\end{cases}
\\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{x_M+x_P}{2}\\
\ \\
\displaystyle y_S = \frac{y_M+y_P}{2}
\end{cases}
$$
R:
\begin{cases}
\displaystyle x_R = \frac{\displaystyle \frac{x_B+x_C}{2}+\frac{x_A+x_D}{2}}{2} \\
\ \\
\displaystyle y_R = \frac{\displaystyle \frac{y_B+y_C}{2}+\frac{y_A+y_D}{2}}{2}
\end{cases}
\\
\ \\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{\displaystyle \frac{x_A+x_B}{2}+\frac{x_C+x_D}{2}}{2} \\
\ \\
\displaystyle y_S = \frac{\displaystyle \frac{y_A+y_B}{2}+\frac{y_C+y_D}{2}}{2}
\end{cases}
$$
R:
\begin{cases}
\displaystyle x_R = \frac{x_aA+x_B+x_C+x_D}{4}\\
\ \\
\displaystyle y_R = \frac{y_A+y_B+y_C+y_D}{4}
\end{cases}
\\
\ \\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{x_A+x_B+x_C+x_D}{4}\\
\ \\
\displaystyle y_S = \frac{y_A+y_B+y_C+y_D}{4}
\end{cases}
$$
\begin{cases}
\displaystyle M\left( \frac{x_A+x_B}{2}, \frac{y_A+y_B}{2} \right)\\
\ \\
\displaystyle N\left( \frac{x_B+x_C}{2}, \frac{y_B+y_C}{2} \right)\\
\ \\
\displaystyle P\left( \frac{x_C+x_D}{2}, \frac{y_C+y_D}{2} \right)\\
\ \\
\displaystyle Q\left( \frac{x_D+x_A}{2}, \frac{y_D+y_A}{2} \right)\\
\end{cases}
$$
Sejam $R$ e $S$ os pontos médio das diagonais $NQ$ e $MP$, respectivamente, do quadrilátero $MNPQ$. Utilizemos novamente a fórmula para o ponto médio de um segmento aplicado às diagonais:
$$R:
\begin{cases}
\displaystyle x_R = \frac{x_N+x_Q}{2}\\
\ \\
\displaystyle y_R = \frac{y_N+y_Q}{2}
\end{cases}
\\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{x_M+x_P}{2}\\
\ \\
\displaystyle y_S = \frac{y_M+y_P}{2}
\end{cases}
$$
Substituindo as coordenadas $(x,y)$ dos pontos $M$, $N$, $P$ e $Q$, temos que:
$$R:
\begin{cases}
\displaystyle x_R = \frac{\displaystyle \frac{x_B+x_C}{2}+\frac{x_A+x_D}{2}}{2} \\
\ \\
\displaystyle y_R = \frac{\displaystyle \frac{y_B+y_C}{2}+\frac{y_A+y_D}{2}}{2}
\end{cases}
\\
\ \\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{\displaystyle \frac{x_A+x_B}{2}+\frac{x_C+x_D}{2}}{2} \\
\ \\
\displaystyle y_S = \frac{\displaystyle \frac{y_A+y_B}{2}+\frac{y_C+y_D}{2}}{2}
\end{cases}
$$
E finalmente obtemos:
$$R:
\begin{cases}
\displaystyle x_R = \frac{x_aA+x_B+x_C+x_D}{4}\\
\ \\
\displaystyle y_R = \frac{y_A+y_B+y_C+y_D}{4}
\end{cases}
\\
\ \\
\ \\
S:
\begin{cases}
\displaystyle x_S = \frac{x_A+x_B+x_C+x_D}{4}\\
\ \\
\displaystyle y_S = \frac{y_A+y_B+y_C+y_D}{4}
\end{cases}
$$
Temos então que as coordenadas $(x,y)$ dos pontos médios das diagonais do quadrilátero $MNPQ$ são iguais e, portanto, os pontos médios $R$ e $S$ são coincidentes. Logo, o quadrilátero $MNPQ$ é um paralelogramo.



Postar um comentário