Podemos demonstrar a relação trigonométrica fundamental utilizando as definições de seno e cosseno e o teorema de Pitágoras.
Uma relação trigonométrica também é conhecida como identidade trigonométrica, porque é verdadeira para qualquer valor do ângulo envolvido.
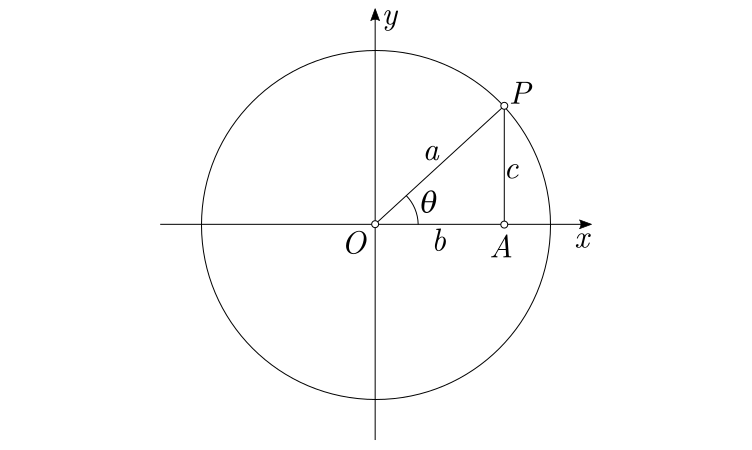
Demonstração 1:
Seja uma circunferência de centro $O$ e um ponto $P$ sobre a circunferência. O segmento $OP=a$ é o raio da circunferência.
A projeção do ponto $P$ sobre os eixos $x$ e $y$ definem um triângulo retângulo de catetos iguais a $b$ e $c$ e hipotenusa igual a $a$.
A definição de seno de um ângulo é dada pela razão entre o cateto oposto pela hipotenusa:
$$\text{sen}(\theta) = \frac{\text{cateto oposto}}{\text{hipotenusa}} = \frac{c}{a} \tag{1}
$$
A definição de cosseno de um ângulo é dada pela razão entre o cateto adjacente pela hipotenusa:
$$\cos(\theta) = \frac{\text{cateto adjacente}}{\text{hipotenusa}} =\frac{b}{a} \tag{2}
$$
Como consequência, a tangente de um ângulo é dada pela razão entre o seno e o cosseno:
$$\text{tg}(\theta) = \frac{\text{sen}(\theta)}{\cos(\theta)} \tag{3}
$$
Aplicando o teorema de Pitágoras no triângulo $OAP$, obtemos:
$$a^2= b^2 + c^2 \tag{4}
$$
Se dividirmos por $a^2$ ambos os membros da relação $(4)$, teremos:
$$\frac{a^2}{a^2} = \frac{b^2}{a^2} + \frac{c^2}{a^2} \tag{ 5}
$$
Aplicando as propriedades da potenciação:
$$1 = \Big( \frac{b}{a}\Big)^2 + \Big(\frac{c}{a}\Big)^2 \tag{6}
$$
Agora, substituímos as relações $(1)$ e $(2)$ em $(6)$:
$$1 = \cos^2(\theta) + \text{sen}^2(\theta) \tag{7}
$$
A relação $(7)$ é conhecida como relação trigonométrica fundamental porque está presente em grande parte de cálculos básicos em trigonometria, como por exemplo, em demonstrações de identidades trigonométricas.
Demonstração 2:
Seja o círculo trigonométrico centrado em $O$ e raio unitário. E seja um ponto $P$ sobre a circunferência. O segmento $OP$ define um ângulo $\theta$ em relação ao eixo dos $x$.
As projeções do ponto $P$ sobre os eixos $x$ e $y$ definem, respectivamente, o cosseno e o seno do ângulo $\theta$.
Aplicando o teorema de Pitágoras no triângulo retângulo $OAP$, obtemos:
$$OP^2 = OA^2 + AP^2\\
\ \\
1 = \cos^2(\theta) + \text{sen}^2(\theta) \tag{8}
$$




Postar um comentário