A lei dos senos (ou teorema dos senos) é uma relação de proporcionalidade válida para quaisquer triângulos, cujos ângulos internos possuam medidas quaisquer.
Dado um triângulo $ABC$, com ângulos internos medindo $\hat{A}$, $\hat{B}$ e $\hat{C}$ e lados $a$, $b$, e $c$, vamos demonstrar que a lei dos senos é dada por:
$$\frac{a}{\text{sen}(\hat{A})} = \frac{b}{\text{sen}(\hat{B})} = \frac{c}{\text{sen}(\hat{C})} = 2R
$$
onde $R$ é o raio da circunferência circunscrita ao triângulo $ABC$.
A Lei dos Senos
A lei dos senos nos garante que em qualquer triângulo o quociente entre cada lado e o seno do ângulo oposto é constante e igual à medida do diâmetro da circunferência circunscrita, ou seja:
$$\frac{a}{\text{sen}(\hat{A})} = \frac{b}{\text{sen}(\hat{B})} = \frac{c}{\text{sen}(\hat{C})} = 2R
$$
Demonstração
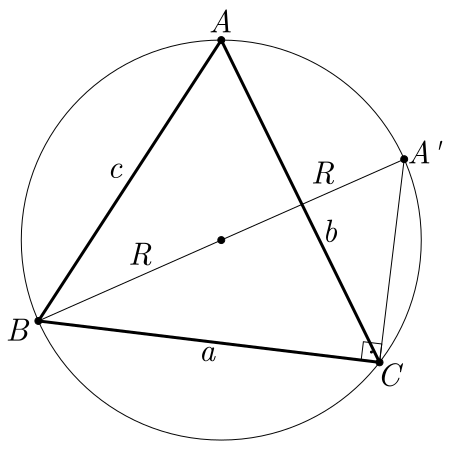
Seja $ABC$ um triângulo qualquer inscrito a uma circunferência de raio $R$.
Por um dos vértices do triângulo (vamos tomar como exemplo o vértice $B$), tracemos o diâmetro da circunferência igual a $\overline{BA^\prime}$ e tracemos o segmento $\overline{A^\prime C}$.
Sabemos que $\hat{A} = \hat{A^\prime}$, pois determinam na circunferência a mesma corda $\overline{BC}$.
O triângulo $A^\prime BC$ é retângulo em $C$ por estar inscrito a uma circunferência.
- Todo triângulo inscrito em uma circunferência onde um dos lados é o diâmetro da circunferência é retângulo, sendo a hipotenusa igual ao diâmetro.
Temos que o seno de um ângulo é definido pela razão do cateto oposto pela hipotenusa. Assim:
$$\text{sen}(\hat{A^\prime}) = \frac{a}{2R}\\
\ \\
a = 2R \cdot \text{sen}(\hat{A^\prime})\\
\ \\
2R = \frac{a}{\text{sen}(\hat{A^\prime})}
$$
Seguindo o mesmo raciocínio, obtemos que:
$$2R = \frac{b}{\text{sen}(\hat{B^\prime})} \quad \text{e}\quad 2R = \frac{c}{\text{sen}(\hat{C^\prime})}
$$
Como as três razões são iguais ao diâmetro $2R$, concluímos que:
$$\frac{a}{\text{sen}(\hat{A})} = \frac{b}{\text{sen}(\hat{B})} = \frac{c}{\text{sen}(\hat{C})} = 2R
$$
Exemplo 1:
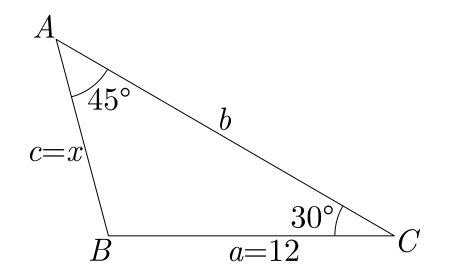
Calcular o valor de $x$ correspondente a um dos lados do triângulo abaixo.
Como temos os lados $a=12$ e $c=x$, e os ângulos $\hat{A}=45°$ e $\hat{C}=30°$, fazemos:
$$\frac{a}{\text{sen}(\hat{A})} = \frac{c}{\text{sen}(\hat{C})}\\
\ \\
\frac{12}{\text{sen}(45°)} = \frac{x}{\text{sen}(30°)}
$$
O seno de $30°=\cfrac{1}{2}$ e o seno de $45°=\cfrac{\sqrt{2}}{2}$, assim:
$$\frac{12}{\displaystyle \frac{\sqrt{2}}{2}} = \frac{x}{\displaystyle \frac{1}{2}}\\
\ \\
\frac{24}{\sqrt{2}} = 2x\\
\ \\
x = \frac{12}{\sqrt{2}}\\
\ \\
x = \frac{12 \sqrt{2}}{2}\\
\ \\
x = 6 \sqrt{2}
$$
Exemplo 2:
Calcular o valor de x correspondente a um dos lados do triângulo abaixo:
A soma dos ângulos internos de um triângulo é igual a $180°$. Assim, o ângulo $\hat{A}$ é dado por:
$$\hat{A} = 180° - (45°+15°)\\
\ \\
\hat{A} = 180° - 60°\\
\ \\
\hat{A} = 120°
$$
O seno de $120°$ encontra-se no segundo quadrante do círculo trigonométrico e quando o reduzimos para o primeiro quadrante, encontramos que $\text{sen}(120°)=\text{sen}(60°)$. Assim:
$$\frac{18}{\text{sen}(60°)} = \frac{x}{\text{sen}(45°)}\\
\ \\
\frac{18}{\displaystyle \frac{\sqrt{3}}{2}} = \frac{x}{\displaystyle \frac{\sqrt{2}}{2}}\\
\ \\
\frac{36}{\sqrt{3}} = \frac{2x}{\sqrt{2}}\\
\ \\
\frac{36 \sqrt{3}}{3} = \frac{2x \sqrt{2}}{2}\\
\ \\
12\sqrt{3} = x\sqrt{2}\\
\ \\
\frac{12\sqrt{3}}{\sqrt{2}} = x\\
\ \\
\frac{12\sqrt{3} \ \sqrt{2}}{2} = x\\
\ \\
x = 6 \sqrt{6}
$$
Exemplo 3:
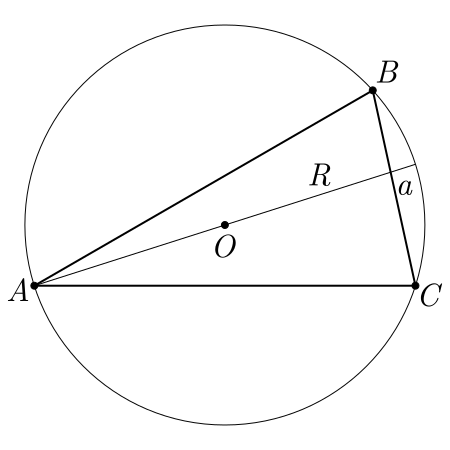
Calcular o raio da circunferência circunscrita a um triângulo $ABC$ em que o lado $a=15$ e o ângulo $\hat{A}=30°$.
Pela lei dos senos, temos que:
$$2R = \frac{a}{\text{sen}(\hat{A})}\\
\ \\
2R = \frac{15}{\text{sen}(30°)}\\
\ \\
2R = \frac{15}{\cfrac{1}{2}}\\
\ \\
2R = 30\\
\ \\
R = 15
$$
Assim, o raio mede 15 unidade de comprimento.
Exemplo 4:
Um professor de Matemática solicitou a seus alunos que formassem grupos para que calculassem a altura de um prédio de 15 andares (considerando o térreo) utilizando um transferidor de grau e a lei dos senos.
Um procedimento adotado por um dos grupos foi de se posicionarem a uma distância do prédio de modo que o ângulo de visão da horizontal até o topo do prédio fosse de $60°$, colocando o transferidor de grau próximo ao olho do observador. Feito isso, mediram a distância entre o observador e a base do prédio, encontrando um valor de $25\ m$. Abaixo encontra-se o esboço do desenho.
Considerando que o triângulo $ABC$, formado pelo observador, a base do prédio e seu topo, é retângulo em $B$, é possível considerá-lo inscrito em uma circunferência cujo segmento $AC$ é a hipotenusa do triângulo $ABC$ e passa pelo centro da circunferência. Aplicando o Teorema de Pitágoras:
$$AC^2 = AB^2 + BC^2 \\
\ \\
(2R)^2 = 25^2 + H^2\\
\ \\
2R = \sqrt{25^5 + H^2}
$$
Pela Lei dos Senos, temos que:
$$\frac{H}{\text{sen}(\theta)} = 2R
$$
Substituindo o valor de $2R = \sqrt{25^5 + H^2}$ na relação acima, obtemos:
$$\frac{H}{\text{sen}(\theta)} = \sqrt{25^5 + H^2}
$$
Como o ângulo $\theta = 60°$, temos que o $\text{sen}(60°)=\cfrac{\sqrt{3}}{2}$. Então:
$$\frac{H}{\cfrac{\sqrt{3}}{2}} = \sqrt{25^5 + H^2}\\
\ \\
\frac{2H}{\sqrt{3}} = \sqrt{ 25^2+H^2}\\
\ \\
2H = \sqrt{3} \sqrt{ 25^2+H^2}\\
\ \\
2H = \sqrt{3 (25^2+H^2)}\\
\ \\
4H^2 = 3(25^2+H^2)\\
\ \\
4H^2 = 3\cdot 25^2 + 3H^2\\
\ \\
H^2 = 3 \cdot 25^2\\
\ \\
H = 25 \sqrt{3}\\
\ \\
H \approx 43,3
$$
Assim, o prédio mede aproximadamente $43,3\ m$ de altura.
Uma estimativa boa é considerar que cada andar de um prédio tenha $3\ m$. Sendo assim, o prédio possui aproximadamente 14,3 andares.
Se desconsiderarmos o erro de observação e as imprecisões das medidas do ângulo e da distância até a base, podemos admitir que os alunos encontraram uma ótima aproximação para a altura do prédio.
Referências:
- Fundamentos de Matemática Elementar V3 - Trigonometria - Gelson Iezzi
- Fundamentos de Matemática Elementar V9 - Geometria Plana - Osvaldo Dolce e Nicolau Pompeo
Links para este artigo:
- https://bit.ly/lei-dos-senos
- https://www.obaricentrodamente.com/2022/01/demonstracao-da-lei-dos-senos-e-algumas-aplicacoes.html
Veja mais:
- Demonstração da lei dos cossenos através do teorema de Pitágoras
- O teorema de Stewart
- Os pontos de Brocard (parte 1)
- Os pontos de Brocard (Parte 2)
- Os pontos de Brocard (Parte 3)




Postar um comentário