Veremos neste artigo dois métodos de como comparar frações para descobrirmos qual delas é a maior e a menor. O método aritmético é o mais eficaz e serve para quaisquer frações; já o método geométrico fica restrito a frações cujos denominadores sejam valores pequenos.
Método aritmético
Para ilustrar o método, vamos comparar as frações $\displaystyle \frac{3}{5}$ e $\displaystyle \frac{5}{7}$ para descobrir qual delas é a maior.
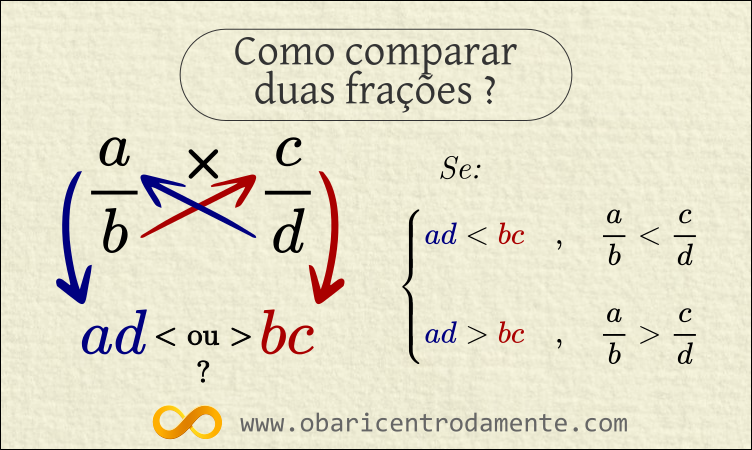
- Escrevemos uma fração ao lado da outra;
- Multiplicamos o denominador da primeira pelo numerador da segunda fração e escrevemos o produto abaixo da segunda (pode ser ao lado ou acima);
- Multiplicamos o denominador da segunda pelo numerador da primeira fração e escrevemos o produto abaixo da primeira;
- A fração que estiver acima do maior produto será a maior fração.
Como $25$ é maior do que $21$, logo, $\displaystyle \frac{5}{7}$ é maior do que $\displaystyle \frac{3}{5}$:
$$\frac{3}{5} < \frac{5}{7}
$$
Justificativa:
Podemos justificar este método encontrando frações equivalentes, cujos denominadores sejam iguais. Uma forma de encontrar frações equivalentes é calcular o menor múltiplo comum $(m.m.c.)$ entre os denominadores das frações dadas.
Para as frações $\displaystyle \frac{3}{5}$ e $\displaystyle \frac{5}{7}$, o $m.m.c.$ entre $5$ e $7$ é $35$. Assim, escrevemos:
$$\frac{}{35} \quad \text{ < ou > } \quad \frac{}{35}
$$
Para descobrirmos os numeradores, dividimos $35$ pelo denominador e multiplicamos o quociente pelo numerador de cada fração dada e escrevemos o produto em cada numerador da fração equivalente:
$$\frac{3\cdot 7}{35} \quad \text{ < ou > } \quad \frac{5 \cdot 5}{35}\\
\ \\
\frac{21}{35} < \frac{25}{35}
$$
Como os denominadores são iguais fica fácil comparar as frações. Assim:
$$\frac{3}{5} < \frac{5}{7}
$$
Método geométrico
Para compararmos duas frações de forma geométrica, podemos representar dois segmentos de reta de comprimentos unitários e dividirmos cada um deles em partes iguais a cada um dos denominadores das frações e tomarmos quantidades iguais a seus numeradores:
Comparando as marcações em cada segmento, podemos ver que a fração $\displaystyle \frac{3}{5}$ é menor do que $\displaystyle \frac{5}{7}$.
Exemplo 1:
Comparar as frações $\displaystyle \frac{5}{7}$ e $\displaystyle \frac{2}{3}$ e verificar qual delas é maior.
Método aritmético:
Como $15$ é maior do que $14$, logo, $\displaystyle \frac{5}{7}$ é maior do que $\displaystyle \frac{2}{3}$:
$$\frac{5}{7} > \frac{2}{3}
$$
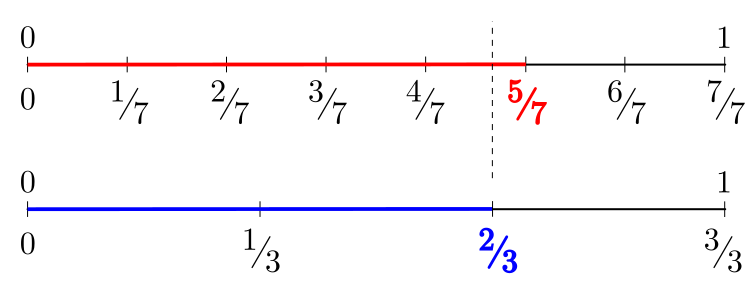
Método geométrico:
Podemos ver que $\displaystyle \frac{5}{7}$ é maior do que $\displaystyle \frac{2}{3}$, mas perceba que a diferença é pequena e se a marcação dos segmentos forem marcadas sem muito critério e de forma imprecisa, pode ficar difícil identificar ou ainda levar ao erro.
Exemplo 2:
Comparar as frações $\displaystyle \frac{12}{67}$ e $\displaystyle \frac{27}{136}$ e verificar qual delas é a maior.
Como $1.809$ é maior do que $1.632$, logo, a fração $\displaystyle \frac{27}{136}$ é maior do que $\displaystyle \frac{12}{67}$:
$$\frac{12}{67} < \frac{27}{136}
$$
Através do método geométrico fica inviável a comparação, pois teríamos que dividir os segmentos unitários em $67$ e $136$ partes iguais. Sendo assim, o ideal é aplicar o método aritmético em todas as situações.
Quando estivermos aprendendo, ou ensinando frações aos alunos, vale a pena explorar o método geométrico para frações com denominadores pequenos, pois possui um apelo visual que pode ser útil na absorção do conhecimento.
Exemplo 3:
Comparar as frações impróprias $\displaystyle \frac{32}{5}$ e $\displaystyle \frac{29}{4}$ e verificar qual delas é a maior.
Neste caso, podemos aplicar diretamente o método aritmético ou reescrever as frações como números mistos:
$$\frac{32}{5} = 6\ \frac{2}{5}\\
\ \\
\text{e}\\
\ \\
\frac{29}{4} = 7\ \frac{1}{4}
$$
Se olharmos a parte inteira de cada número misto acima, vemos que o segundo possui a parte inteira maior que a primeira. Logo, a segunda fração é maior que a primeira:
$$\frac{32}{5} < \frac{29}{4}
$$
Se aplicarmos o método aritmético:







Postar um comentário