Na Grécia antiga do século V a.C., os matemáticos comparavam grandezas de mesma espécie e expressavam a razão entre as medidas de dois segmentos de reta com um número racional. Eles acreditavam que sempre haveria um terceiro segmento que caberia um número inteiro de vezes simultaneamente em ambos os segmentos.
No entanto, quando tentaram comparar os segmentos que formavam os lados de um quadrado de comprimento igual a $1$ com sua diagonal, uma dúvida surgiu: Será que a razão entre as medidas do lado e da diagonal de qualquer quadrado poderia ser expressa através de um número racional?
Expressando a razão entre medidas de segmentos
Vamos considerar dois segmentos de reta $AB$ e $CD$, cujas medidas são $8\ u.c.$ e $5\ u.c.$, respectivamente.
A razão entre as medidas dos dois segmentos pode ser expresso como:
$$\frac{AB}{CD} = \frac{8}{5}
$$
A razão $\displaystyle \frac{8}{5}$ é um número racional e, sendo assim, existe um terceiro segmento $EF$ que cabe um número inteiro de vezes em ambos os segmentos. A este terceiro segmento, damos o nome de $m.d.c.$ (maior divisor comum).
- Leia o artigo: Algoritmo de Euclides para o cálculo do m.d.c.
Como as medidas dos segmentos $AB$ e $CD$ são primos entre si, ou seja, somente o número $1$ divide $8$ e $5$ simultaneamente, o segmento que cabe um número de vezes tanto em $AB$ quanto em $CD$ é o segmento $EF$ de medida igual a $1$.
Exemplo 1:
Vamos utilizar o procedimento dos gregos antigos para encontrar um terceiro segmento $EF$ que caiba um numero inteiro de vezes tanto em $AB=6$ e em $CD=2$.
Iniciamos representando os segmentos $AB$ e $CD$ dividindo-os em unidades:
A razão entre as medidas dos segmentos é dada por:
$$\frac{AB}{CD} = \frac{6}{2} = 3
$$
$\longrightarrow$ Lê-se: $AB$ está para $CD$, assim como $6$ está para $2$.
Isso quer dizer que o segmento $AB$ é igual a $3$ vezes o segmento $CD$:
$$\frac{AB}{CD} = 3\\
\ \\
AB = 3\ CD
$$
Como o segmento $CD=2$, logo, $AB = 6$.
Mas, se expressarmos a razão de forma invertida, teremos:
$$\frac{CD}{AB} = \frac{2}{6} = \frac{1}{3}
$$
Isso quer dizer que o segmento $CD$ é igual a $1/3$ do segmento $AB$. O que não altera as medidas dos segmentos, mas apenas é visto sob outra perspectiva.
Os segmentos que cabem simultaneamente um número inteiro de vezes tanto em $AB$ quanto em $CD$ são os segmentos de:
- $1$ unidade de comprimento
- $2$ unidades de comprimento
Tomamos o maior segmento como o maior divisor comum entre $AB$ e $CD$. Assim:
$$m.d.c.(6,2)=2
$$
Cálculo do $m.d.c.$ pelo processo de subtrações sucessivas
Este processo para calcular o $m.d.c.$ entre dois segmentos de reta pode ser aplicado na forma geométrica ou aritmética.
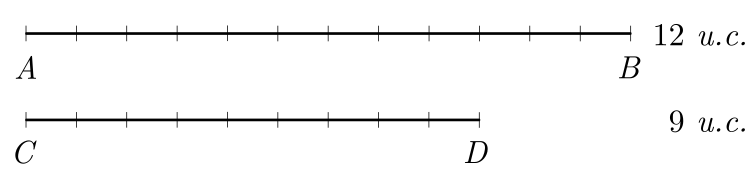
Vamos supor dois segmentos de comprimentos iguais a $AB=12\ u.c.$ e $CD=9\ u.c.$. Queremos encontrar um terceiro segmento que caiba um número de vezes tanto em $AB$ quanto em $CD$.
Iniciamos representando os dois segmentos:
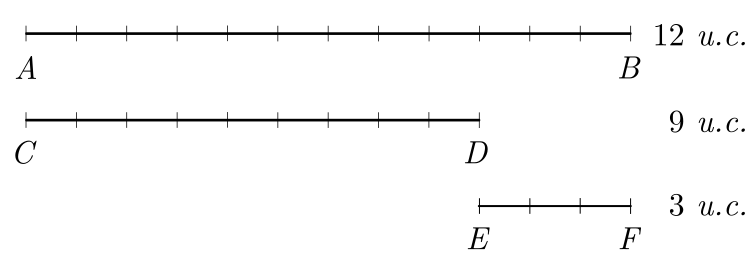
Subtraímos o segmento menor do maior, fazendo: $AB-CD$:
Prosseguimos desprezando o maior segmento e realizamos uma nova subtração, fazendo $CD-EF$:
Prosseguimos desprezando o maior segmento e realizamos a nova subtração $GH-EF$:
Prosseguimos desprezando o maior segmento e realizamos a nova subtração: $EF=IJ$:
Quando encontramos uma diferença nula (isso ocorre porque ambos os segmentos são congruentes), paramos o processo e tomamos o último segmento $IJ$ como o maior divisor comum entre os segmentos originais $AB$ e $CD$. Sendo assim, o segmento $IJ=3\ u.c.$ é o $m.d.c.$ entre os segmentos $AB=12\ u.c.$ e $CD=9\ u.c.$:
$$m.d.c.(12,9) = 3
$$
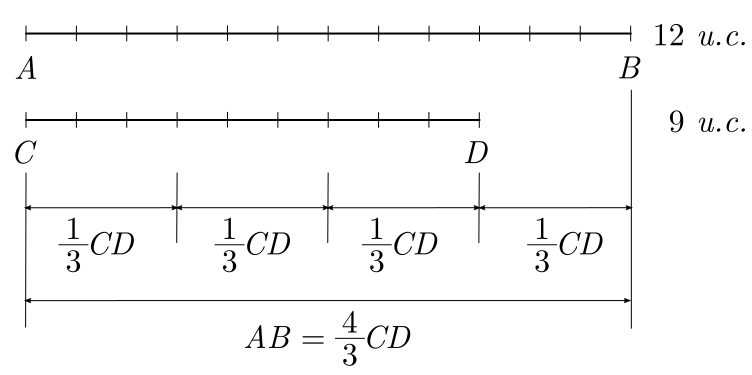
A razão entre os segmentos $AB=12\ u.c.$ e $CD=9\ u.c.$ é dada por:
$$\frac{AB}{CD} = \frac{12}{9} = \frac{4}{3}
$$
Isso significa que o segmento $AB$ possui comprimento igual a $4/3$ do segmento $CD$. Como $4/3$ é igual a $1$ inteiro mais $1/3$, o segmento $AB$ é igual ao segmento $CD$ mais $1/3$:
Cálculo do $m.d.c.$ entre números naturais pelo método das subtrações sucessivas
Vamos utilizar a mesma ideia das subtrações sucessivas, mas de forma aritmética, para calcular o $m.d.c.$ entre os números $12$ e $9$. O procedimento é semelhante ao geométrico realizado anterior mente.
Seja calcular o maior divisor comum entre os números $12$ e $9$:
$$m.d.c.(12,9)
$$
Subtraímos o menor do maior número:
$$12 - 9 = 3
$$
Desprezamos o maior número (que no caso é o $12$) e realizamos uma nova subtração:
$$9 - 3 = 6
$$
Desprezamos o maior número (que no caos é o $9$) e realizamos uma nova subtração:
$$6-3=3
$$
Desprezamos o maior número e realizamos uma nova subtração:
$$3-3=0
$$
Como obtivemos uma diferença igual a $0$, paramos o processo e tomamos o último número como o maior divisor comum (que no caos é o $3$). Assim:
$$m.d.c.(12,9)=3
$$
Observamos que os valores encontrados nos processos geométrico e aritmético foram os mesmo, o que não espanta, mas conforta.
Exercícios
Realizar os processos das subtrações sucessivas na forma geométrica e aritmética para encontrar o maior divisor comum entre os segmentos:
a) $m.d.c.(10,4)$
b) $m.d.c.(6,3)$
c) $m.d.c.(7,5)$
d) $m.d.c.(20,8)$
e) $m.d.c.(16,12)$
Cálculo do $m.d.c.$ entre números decimais
Podemos aplicar o método das subtrações sucessivas para calcular o $m.d.c.$ entre números decimais da mesma forma que fizemos com o processo aritmético.
Vamos calcular o $m.d.c.$ entre os números $1,2$ e $3,4$. Subtraímos sempre o menor do maior e na próxima etapa, desprezamos o numero maior.
$$3,4 - 1,2 = 2,2\\
\ \\
2,2 - 1,2 = 1,0\\
\ \\
1,2 - 1,0 = 0,2\\
\ \\
1,0 - 0,2 = 0,8\\
\ \\
0,8 - 0,2 = 0,6\\
\ \\
0,6 - 0,2 = 0,4\\
\ \\
0,4 - 0,2 = 0,2\\
\ \\
0,2 - 0,2 = 0
$$
Assim, o $m.d.c.(1,2 ; 3,4) = 0,2$.
Tente encontrar através do método das subtrações sucessivas o $m.d.c.$ entre os números $9,7$ e $6,8$.
Cálculo do $m.d.c.$ entre números racionais
Se quisermos calcular o $m.d.c.$ entre duas quantidades racionais, ou seja, que podem ser expressas sob a forma de fração, podemos também aplicar o método das subtrações sucessivas.
Uma dificuldade que pode surgir é a comparação entre as frações para identificar qual delas é a maior ou a menor.
Antes de iniciar com o processo para o cálculo do $m.d.c.$ entre frações, vamos ver dois métodos comparativos:
1) Método aritmético:
Se quisermos saber, por exemplo, entre as frações $\displaystyle \frac{3}{5}$ e $\displaystyle \frac{5}{7}$ qual é a maior, podemos fazer:
Multiplicamos em cruz, e escrevemos os resultados logo abaixo, como mostrado na figura acima. Comparando os produtos ($21$ e $25$), vemos que $25$ é maior do que $21$, logo, a fração $\displaystyle \frac{5}{7}$ é maior do que a fração $\displaystyle \frac{3}{5}$.
2) Método geométrico:
Podemos representar em um segmento de reta como sendo $1$ inteiro e subdividimos o segmento em partes iguais ao denominador da fração e tomamos a quantidade igual ao numerador. Fazemos isso para as duas frações e comparamos qual é a maior:
Podemos ver a fração $\displaystyle \frac{5}{7}$ é maior do que a fração $\displaystyle \frac{3}{5}$.
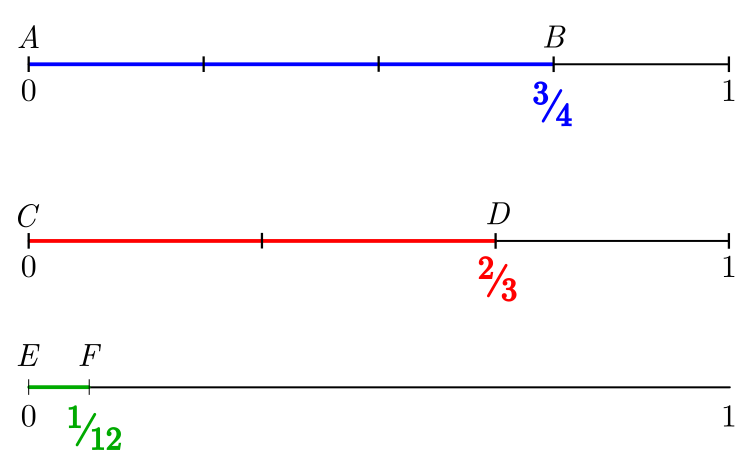
Vamos calcular o $m.d.c.$ entre os segmentos $\displaystyle AB=\frac{3}{4}$e $\displaystyle CD=\frac{2}{3}$ através do processo de subtrações sucessivas.
Iniciamos subtraindo a menor da maior fração. Após identificar qual delas é a maior, realizamos a subtração entre elas. Nas etapas seguintes, desprezamos a maior fração e seguimos com as subtrações:
$$\frac{3}{4} - \frac{2}{3} = \frac{3\cdot 3 - 4\cdot 2}{12} = \frac{9-8}{12} = \frac{1}{12}\\
\ \\
\frac{2}{3} - \frac{1}{12} = \frac{2\cdot 4 - 1}{12} = \frac{8-1}{12} = \frac{7}{12}\\
\ \\
\frac{7}{12} - \frac{1}{12} = \frac{7-1}{12} = \frac{6}{12}\\
\ \\
\frac{6}{12} - \frac{1}{12} = \frac{6-1}{12} = \frac{5}{12}\\
\ \\
\frac{5}{12} - \frac{1}{12} = \frac{5-1}{12} = \frac{4}{12}\\
\ \\
\frac{4}{12} - \frac{1}{12} = \frac{4-1}{12} = \frac{3}{12}\\
\ \\
\frac{3}{12} - \frac{1}{12} = \frac{3-1}{12} = \frac{2}{12}\\
\ \\
\frac{2}{12} - \frac{1}{12} = \frac{2-1}{12} = \frac{1}{12}\\
\ \\
\frac{1}{12} - \frac{1}{12} = 0
$$
Assim, encontramos que $\displaystyle \frac{1}{12}$ é o $m.d.c.$ entre os segmentos de medidas $\displaystyle AB=\frac{3}{4}$ e $\displaystyle CD = \frac{2}{3}$:
$$m.d.c. \left( \frac{3}{4},\frac{2}{3}\right) = \frac{1}{12}
$$
Isso quer dizer que o maior segmento que cabe um número inteiro de vezes tanto em $AB$ quanto em $CD$ é o segmento de comprimento igual a $\displaystyle \frac{1}{12}$.
A razão entre as medidas dos segmentos $AB$ e $CD$ é dada por:
$$\frac{AB}{CD} = \frac{\ \displaystyle \frac{3}{4} \ }{ \displaystyle\frac{2}{3} }\\
\ \\
\frac{AB}{CD} = \frac{3}{4} \cdot \frac{3}{2}\\
\ \\
\frac{AB}{CD} = \frac{9}{8}\\
\ \\
\frac{AB}{CD} = 1+\frac{1}{8}
$$
Isso quer dizer que o segmento $AB$ é igual ao comprimento de $CD$ mais $1/8$:
$$AB = CD\left(1+\frac{1}{8}\right)\\\ \\
AB = CD+\frac{1}{8}CD
$$
Por outro lado, se fizermos:
$$\frac{CD}{AB} = \frac{\ \displaystyle \frac{2}{3}\ }{\displaystyle \frac{3}{4} }\\
\ \\
\frac{CD}{AB} = \frac{2}{3}\cdot \frac{4}{3}\\
\ \\
\frac{CD}{AB} = \frac{8}{9}
$$
Isso quer dizer que o segmento $CD$ é igual a $8/9$ do segmento $AB$:
$$
CD = \frac{8}{9}AB
$$
CD = \frac{8}{9}AB
$$
Segmentos comensuráveis e incomensuráveis
Todos os exemplos anteriores foram realizados com números racionais, ou seja, números que podem ser expressos sob a forma de fração. Desta forma, podemos observar que:
- Dados dois segmentos cujas medidas dos comprimentos são números racionais, existe sempre um terceiro segmento que cabe um número inteiro de vezes nos dois segmentos dados, ou seja, esse terceiro segmento determina uma unidade de medida comum aos dois segmentos.
- O maior segmento que cabe nos dois segmentos dados é o $m.d.c.$ entre eles.
- É sempre possível medir um segmento em função do outro, pois existe uma razão entre as medidas desses segmentos. Se $m$ é a medida do segmento $AB$ e $n$ é a medida do segmento $CD$, podemos encontrar a razão entre esses segmentos fazendo:
$$
\frac{AB}{CD} = \frac{m}{n}
$$
\frac{AB}{CD} = \frac{m}{n}
$$
Se dois segmentos obedecem às condições anteriores, podemos dizer que são segmentos comensuráveis, ou seja, eles constituem grandezas comensuráveis, ou seja, são segmentos que podem ser medidos e determinados em relação a uma unidade previamente fixada (razão).
Podemos verificar se dois segmentos são comensuráveis se existir segmentos divisores comuns entre eles, geometricamente através de compasso, ou aritmeticamente através da existência de um $m.d.c.$ entre as medidas desses segmentos.
Se tomarmos um quadrado de lado igual a $1$, podemos aplicar o Teorema de Pitágoras e obtermos a medida da diagonal igual a $\sqrt{2}$:
$$
d^2 = 1^2+1^2\\
\ \\
d^2 = 1+1\\
\ \\
d^2=2\\
\ \\
d=\sqrt{2}
$$
d^2 = 1^2+1^2\\
\ \\
d^2 = 1+1\\
\ \\
d^2=2\\
\ \\
d=\sqrt{2}
$$
A raiz quadrada de $2$, assim como qualquer raiz quadrada de um número que não seja um quadrado perfeito, é um número irracional e, portanto, não pode ser expresso sob a forma de uma fração do tipo $\displaystyle \frac{m}{n}$, sendo $m$ e $n$ dois números inteiros, ou em outras palavras, não existe dois números inteiros que expressem a razão entre o comprimento dos lados e a diagonal do quadrado de lado igual a $1$. Isso ocorre porque $\sqrt{2}$ é um número irracional e sua parte decimal é uma dízima infinita não periódica e, não é possível aplicar o processo das subtrações sucessivas.
Dizemos que se trata de grandezas incomensuráveis e, por isso, se entre dois segmentos houver um número irracional, serão segmentos incomensuráveis.
Desta forma, nem sempre conseguiremos medir um seguimento tomando outro como unidade e medida.
Este foi o marco na vida dos pitagóricos, pois ele conheciam apenas os números racionais e contrariavam as resoluções geométricas que utilizavam, levando a uma crise no desenvolvimento da Matemática na escola pitagórica, o que levou à descoberta de um conjunto de números até então desconhecido: Os Números Irracionais.
Exercícios:
1) Para cada um dos pares de segmentos comensuráveis dados abaixo, determinar aritmeticamente o $m.d.c.$ entre eles e a razão entre a medida do maior e do menor.
a) $AB = 0,666\cdots$ e $CD=0,5$
b) $EF = 2,5$ e $GH = 1,5$
c) $IJ = 0,555\cdots $ e $KL = \displaystyle \frac{1}{2}$
d) $MN = 0,75$ e $OP = \displaystyle \frac{5}{6}$
2) Em cada item, indicar um par de segmentos comensuráveis e um par de segmentos incomensuráveis:
a) Em um triângulo retângulo, a hipotenusa mede $8\ cm$ e um dos catetos mede $5\ cm$.
b) Em um triângulo isósceles, os lados congruentes medem $12\ cm$ e a base mede $10\ cm$.
c) Em um retângulo, os lados medem $16\ cm$ e $10\ cm$.
3) Calcular por subtrações sucessivas o $m.d.c.$ entre os números indicados:
a) $100$ e $75$
b) $248$ e $36$
c) $900$ e $320$
Referências:
- Apostila Anglo, 9º Ano, Caderno 1




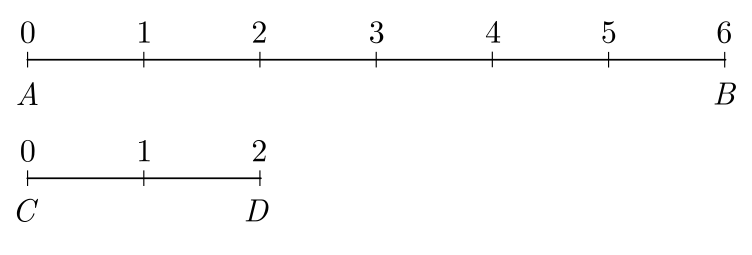






Postar um comentário