Bonaventura Cavalieri nasceu em Milão em 1598. Foi aluno de Galileu e atuou como professor da Universidade de Bolonha de 1629 até 1647, ano de sua morte.
A grande contribuição de Cavalieri à Matemática é o tratado Geometria indivisibilibus de 1635. Neste tratado é apresentado o seu método dos indivisíveis, cuja motivação direta se encontre nas tentativas de Kepler de achar certas áreas e certos volumes.
No entanto, é um pouco difícil de descobrir o que ele entendia por "indivisível". Tudo indica que um indivisível de uma porção plana dada é uma corda dessa porção e o indivisível de um sólido é uma secção desse sólido. Considera-se que uma porção plana seja formada por infinitas cordas paralelas. Então, argumentava Cavalieri, fazendo deslizar cada um dos elementos do conjunto das cordas paralelas de uma porção plana dada ao longo de seu próprio eixo, de modo que as extremidades das cordas ainda descrevam um contorno contínuo, a área da nova porção plana é igual à original, uma vez que ambas são formadas pelas mesmas cordas.
Um procedimento análogo pode ser aplicado a um sólido, formado por secções planas e paralelas. Que fornecerá um novo sólido com mesmo volume. Uma ilustração deste resultado pode ser demonstrada utilizando duas pilhas de moedas de mesmo formato: a primeira pilha fazendo um cilindro reto e a segunda com suas laterais deformadas:
[Figura 1: sólidos com moedas]
Obviamente que os volumes serão os mesmos, independentemente da geometria obtida pela deformação na segunda pilha de moedas, uma vez que são utilizadas moedas do mesmo formato e quantidades iguais para cada pilha.
Esses resultados, ligeiramente generalizados, fornecem os chamados Princípios de Cavalieri, que podem ser enunciados como:
1) Se duas porções planas são tais que toda reta secante a elas e paralela a uma reta dada determina nas porções segmentos de reta cuja razão é constante, então, a razão entre as áreas dessas porções é a mesma constante. E isso nos leva a dizer que as áreas das duas porções são iguais.
2) Se dois sólidos são tais que todo plano secante a eles e paralelo a um plano dado determina nos sólidos secções cuja razão é constante, então a razão entre os volumes desses sólidos é a mesma constante. Em outras palavras: dois sólidos com a mesma altura têm o mesmo se seccionados por um plano paralelo ao plano onde estão assentados, geram áreas iguais.
[Figura 2: comparação de dois sólidos]
Para ilustrar o Princípio de Cavalieri, primeiramente vamos tomar o caso de porções planas, determinando a área compreendida por uma elipse de semieixos $a$ e $b$. Considere a elipse:
\begin{equation}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \:, \: \text{sendo}\: a>b
\end{equation}
E a circunferência:
\begin{equation}
x^2+y^2=a^2
\end{equation}
onde $a$ é o raio da circunferência.
Sendo as duas referidas ao mesmo sistema de coordenadas retangulares:
[Figura 3: circunferência e elipse]
Podemos reescrever a equação da elipse em função de $y$. Tomamos a equação $(1)$:
\begin{equation*}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{equation*}
Encontramos o $mmc$:
\begin{equation*}
\frac{x^2b^2+y^2a^2}{a^2b^2}=1
\end{equation*}
Desenvolvendo:
\begin{equation*}
x^2b^2+y^2a^2 = a^2b^2\\
y^2a^2 = a^2b^2 - x^2b^2\\
y^2 = \frac{b^2(a^2-x^2)}{a^2}
\end{equation*}
Chegando finalmente a:
\begin{equation}
y = \frac{b}{a} \cdot \sqrt{a^2 - x^2}
\end{equation}
Agora, reescrevemos a equação da circunferência em função de $y$:
\begin{equation*}x^2+y^2=a^2\\
y^2=a^2-x^2
\end{equation*}
Encontrando:
\begin{equation}
y=\sqrt{a^2-x^2}
\end{equation}
Substituindo $(4)$ em $(3)$:
\begin{equation}
\sqrt{a^2-x^2}=\frac{b}{a} \cdot \sqrt{a^2-x^2}
\end{equation}
Vemos que a razão entre duas ordenadas correspondentes quaisquer da elipse e da circunferência é $b/a$. Pelo Princípio de Cavalieri concluímos que:
\begin{equation}
A_{\: \text{elipse}} = \frac{b}{a} \cdot A_{\: \text{círculo}}
\end{equation}
\begin{equation}
A_{\: \text{elipse}} = \frac{b}{a} \cdot A_{\: \text{círculo}}
\end{equation}
Hoje, fica fácil de verificar: sabemos que a área da elipse é dada por $A_{\: \text{elipse}}=\pi ab$ e a área do círculo é dada por $A_{\: \text{círculo}}=\pi a^2$. Substituindo na relação $(6)$, obtemos:
\begin{equation}\pi ab = \frac{b}{a} \pi a^2
\end{equation}
Portanto, a razão entre duas cordas verticais correspondentes da elipse e da circunferência é $b/a$.
Agora, podemos demonstrar o Princípio de Cavalieri aplicado a sólidos para verificar o volume de uma esfera de raio $r$.
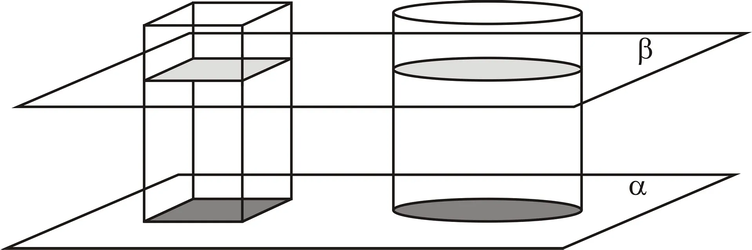
Considere na figura $4$ uma esfera de raio $r$ e uma anticlepsidra (sólido geométrico gerado a partir de um cilindro equilátero onde se subtrai dois cones opostos pelo vértice cujas bases coincidem com as bases do cilindro), assentados num mesmo plano$\alpha$. Seccionando ambos sólidos com um plano $\beta$ paralelo ao plano $\alpha$ a uma altura $h$ dos vértices dos cones:
[Figura 4: Esfera e a anticlepsidra]
Esse plano $\beta$ secciona esfera gerando um círculo de raio s e a anticlepsidra gerando uma coroa circular.
Utilizando da geometria elementar, vamos mostrar que ambas as secções têm área igual a $\pi (r^2-h^2)$.
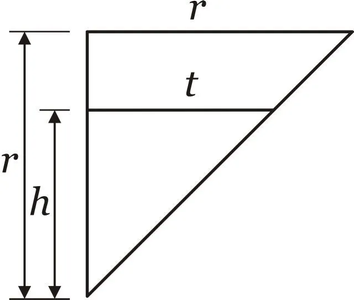
Da esfera, podemos destacar o triângulo retângulo abaixo e utilizar o Teorema de Pitágoras para escrever o raio $s$ em função de $r$ e $h$.
[Figura 5: triângulo retângulo]
\begin{equation}
r^2=h^2+s^2 \Longrightarrow s^2=r^2-h^2
\end{equation}
A área da secção circular será dada por:
\begin{equation}
A=\pi s^2
\end{equation}
Substituindo $(8)$ em $(9)$, obtemos:
\begin{equation}
A=\pi(r^2-h^2)
\end{equation}
Agora falta mostrar que a área da coroa circular é igual à área da secção circular. Da anticlepsidra destacamos o triângulo retângulo:
[Figura 6: triângulo retângulo]
Por semelhança de triângulos temos que:
\begin{equation}\frac{r}{h}=\frac{r}{t}
\end{equation}
Segue que
\begin{equation}
t=h
\end{equation}
A área da coroa será dada pela diferença entre a área do círculo de raio $r$ e o círculo de raio $t$:
\begin{equation}A_C=\pi r^2 - \pi t^2
\end{equation}
Substituindo $(12)$ em $(13)$, obtemos:
\begin{equation}
A_C=\pi (r^2-h^2)
\end{equation}
Provamos que as áreas das secções geradas pelo plano $\beta$ nos sólidos são iguais. Segue-se, então, que pelo Princípio de Cavalieri, que os dois sólidos têm volumes iguais. Logo o volume $V$ da esfera é igual ao volume $V$ da anticlepsidra:
\begin{equation}
V_{esfera} = V_{cilindro} - 2V_{cone} = A_b \cdot - 2\cdot \frac{A_b \cdot h}{3}
\end{equation}
\begin{equation}
V_{esfera} = V_{cilindro} - 2V_{cone} = A_b \cdot - 2\cdot \frac{A_b \cdot h}{3}
\end{equation}
\begin{equation}
V_{esfera}=\pi r^2 \cdot 2r - \frac{2}{3}\cdot \pi r^2 \cdot r = 2\pi r^3- \frac{2}{3} \pi r^3 = \frac{4}{3} \pi r^3
\end{equation}
O que é feito no Princípio de Cavalieri é uma comparação entre dois sólidos. Mas, temos que escolher convenientemente esses sólidos para obtermos resultados satisfatórios. Vejam que, se compararmos dois prismas, se seccionarmos por um plano paralelo em qualquer altura dos sólidos as áreas geradas serão constantes:
[Figura 7: Comparação entre dois prismas]
No caso de uma comparação entre duas pirâmides seccionadas por planos paralelos, notamos que quanto mais próximo do vértice os sólidos forem seccionados por um plano paralelo, menor será a área gerada. No entanto, esta variação na área será constante para as duas pirâmides. Podemos dizer que a área da secção será $kA_b$ onde $k$ é uma constante e $A_b$ é a área da base. Então a área de cada secção será variável para cada ponto da altura da pirâmide:
[Figura 8: Comparação entre duas pirâmides]
Mas, se tomarmos um prisma e uma pirâmide, o Princípio de Cavalieri falha, justamente porque no prisma a área gerada será a mesma independentemente de onde o plano seccioná-lo e já na pirâmide a área gerada será variável, o que torna o método inconsistente. Vejam que, se tomarmos o raio $r$ da base dos dois sólidos como iguais, no cilindro as áreas geradas pelos planos $\beta$ e $\gamma$ são iguais à da base. Já na pirâmide as áreas geradas pelos planos $\beta$ e $\gamma$ são diferentes, diminuindo ao se aproximar do vértice.
[Figura 9: comparação entre prisma e pirâmide]
Os Princípios de Cavalieri representam ferramentas poderosas para o cálculo de áreas, volumes e ademais, sua base intuitiva pode facilmente tornar-se vigorosa com o cálculo integral moderno. Com a aceitação desses princípios como evidentes, intuitivamente, podem-se resolver muitos problemas de mensuração que normalmente requeriam técnicas avançadas de cálculo.
Referências:
- Introdução à História da Matemática - Howard Eves
- Notas de aulas









Realmente muito interessante, nunca tinha ouvido falar sobre estes princípios... A comparação com a pilha de moedas foi genial, meus parabéns!
ResponderExcluirUm abraço!
Marcelo Flora
================
MF Matemática: http://www.mfmatematica.blogspot.com
Que bom que gostou, pois vindo de você é um ótimo elogio. Um abraço amigo!
ResponderExcluirEu sempre venho ler os seus posts que estão cada vez melhores. Eu escrevi a algum tempo um post em que usa o Principio de Cavalieri. Veja mais aqui
ResponderExcluirhttp://fatosmatematicos.blogspot.com/2009/07/volume-do-elipsoide-pelo-principio-de.html
sem entrar em detalhes do método, mas o seu post ficou perfeito. Está de parabénns!!
Obs. Para dar volume de seguidores, ti convido a seguir o meu, que eu sigo o seu blog.
Abraços!!
Olá Prof. Sinceramente pensava que já era seguidor do Fatos, mas já estou te seguindo.
ResponderExcluirObrigado pelo elogio sobre este post, pois minha idéia era abranger o maior número de informações. Mas sempre falta alguma coisa e acho que o seu post sobre o assunto incrementa mais (vou ler com mais calma). Vou colocar um link no corpo do post.
Um abraço!!
Até+
Obrigado por citar no corpo do texto. Vou escrever um post fazendo referencia de algum post seu tambem.
ResponderExcluirAbraços!
Legal professor, acho muito saudável essa troca.
ResponderExcluirAbraços!
Até+
Realmente um ótimo post. Muito bem detalhado. Creio que foi o melhor artigo que encontrei na net sobre o assunto.
ResponderExcluirÓtimo artigo. Me ajudou muito!!!
ResponderExcluirMax
Valeu cara. Ficou muito bom. As figuras também esstão ótimas!! Abraço! Jedi
ResponderExcluirqueria saber uns questoes q a minha prof passou sera q vcs tem como me ajudar ? ela pidiu
ResponderExcluiroq é o principio de cavalieri e piramides
quem é cavalieri ?
quais sao os elementos q compoem uma pirâmide ?
como sao clasificadas as piramides ?
Olá Erika,Vamos lá:
ResponderExcluirQuem foi Cavalieri? Tem uma breve descrição no começo deste artigo. Você pode encotrar mais aqui:
http://pt.wikipedia.org/wiki/Bonaventura_Cavalieri
O que é o Princípio de Cavalieri? Este Princípio é a grosso modo, uma comparação entre dois sólidos, onde, para verificar sua eficácia, é garantido que: dois sólidos de mesma altura terão o mesmo volume, se uma secção plana e paralela às bases geram uma mesma área em cada sólido. Para esta demonstração, veja o artigo acima.
Elementos e classificações de pirâmide: veja um estudo aqui: http://pessoal.sercomtel.com.br/matematica/geometria/piramide/piramide.htm
E veja a demonstração do Volume de pirâmide aqui:
http://obaricentrodamente.blogspot.com/2009/06/demonstracao-da-formula-do-volume-de.html
Nossa! Excelente artigo Kleber!Tirou todas minhas dúvidas.
ResponderExcluirBjs
Mirka ;)
professor em ajuda =(
ResponderExcluir???
ResponderExcluirincrivel bem explicativo
ResponderExcluirinteressante....
parabéns compriu com sua meta
ass: prity :-)
Fiz uma referência a este artigo em
ResponderExcluirhttp://serolmar.wordpress.com/2011/12/01/o-numero-de-n-faces-de-um-n-cubo/
por considerar que explica, de uma forma clara e sucinta o princípio de Cavalieri. Considerei uma generalização a um número superior de dimensões para determinar o volume de um simplex. Trata-se, de facto, de uma pérola da época anterior ao desenvolvimento do cálculo com Leibnitz e Newton.
Linda a Matemática. Parabéns pelo blog!
ResponderExcluira matemática é o ápice da vida..
ResponderExcluirprezado professor
ResponderExcluirestava passeando em seu blog quando deparei com este artigo. faço um comentário bastante atrasado, porem acredito que será útil.
acabei de ler um excelente livro denominado " how a dangerous mathematical theory shaped the modern word" o autor é amir alexander.
este livro trata do inicio do desenvolvimento daquilo que hoje é denominado de calculo diferencial e integral. porem o autor não trata o assunto matematicamente e sim desenvolve o tema por um cenário político e religioso. neste livro somos apresentados aos matemáticos que iniciaram ou apoiaram estes estudos , como galileu, cavalieri, clavius e outros. o autor apresenta também o papel da igreja católica, no trabalho dos jesuitas no impedimento destes estudos. hoje é dificil de acreditar mas os jesuitas eram totalmente contrários ao estudo dos indivisíveis.
Muito obrigada!! Seu post está me ajudando muito para uma apresentação na escola, espero me sair bem ;)
ResponderExcluir