O Teorema de Faure

O Teorema de Faure (ou Fauro) é uma relação métrica da circunferência, relacionando o raio com duas cordas perpendiculares onde o ponto de intersecção definem 4 segmentos de modo que a soma dos quadrados dos segmentos é igual a quatro vezes o quadrado do raio:

$$
a^2+b^2+c^2+d^2=4r^2 \tag{1}
$$

Para demonstrar o Teorema de Faure, utilizaremos o Teorema das cordas e o Teorema de Pitágoras.

Antes de iniciarmos a demonstração, vamos relembrar alguns conceitos:

Definição 1: Circunferência

A circunferência é o conjunto de pontos equidistante a um ponto fixo no plano. Ou seja, dado um ponto $O$, os pontos que estão a uma distância $r$ formam a circunferência. Ou ainda, em outras palavras, é o contorno de um círculo.

Definição 2: Corda

Corda é um segmento de reta que une dois pontos localizados em uma circunferência. Se uma corda passa pelo centro $O$ da circunferência, essa corda recebe um nome especial, chamada de diâmetro, e representada pela letra $d$.

Teorema 1: Teorema das Cordas

Se uma reta passa por um ponto $P$ e corta uma circunferência nos pontos $A$ e $B$, então o produto $PA \cdot PB$ é constante.

Vamos considerar apenas o caso em que o ponto $P$ é interior à circunferência. Assim, temos que a corda $AB$ passa por $P$. Seja uma segunda corda $CD$ passando por $P$.

A partir dessas duas cordas, podemos definir dois triângulos compartilhando o mesmo vértice $P$. Se provarmos que esses dois triângulos são semelhantes, conseguimos provar o teorema das cordas.

Como os dois triângulos compartilham o mesmo vértice $P$, os ângulos $A\hat{P}D$ e $C\hat{P}B$ são congruentes.

Por outro lado, os ângulos $A\hat{D}P$ e $C\hat{B}P$ também são congruente, pois determinam o mesmo arco $AC$. Estes ângulos são inscritos e suas medidas são iguais à metade o ângulo central.

• Leia o artigo: O teorema do ângulo inscrito

Assim, temos que os triângulos $APD$ e $CPB$ são semelhantes pelo caso ângulo-ângulo (AA). Logo:

$$
\frac{PA}{PC} = \frac{PD}{PB} \tag{2}
$$
O que nos leva a:
$$
PA \cdot PB = PC \cdot PD \tag{3}
$$
Assim, o produto $PA \cdot PD$ é constante.

Teorema 2: O Teorema de Faure

Vamos iniciar construindo uma circunferência e duas cordas perpendiculares em $P$, dividindo as cordas $AB$ e $CD$ em segmentos $a$ e $b$ e $c$ e $d$, respectivamente. Traçamos dois segmentos perpendiculares às cordas partindo do centro $O$ da circunferência, cortando-as em seus pontos médios $M$ e $N$.

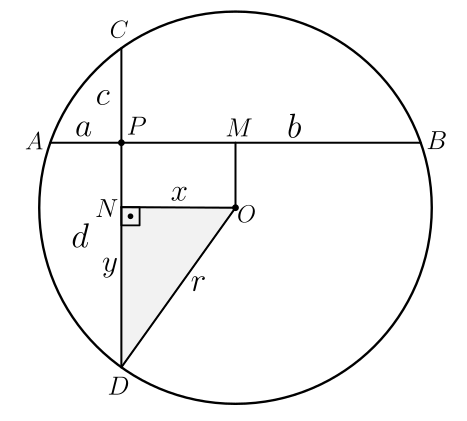
Vamos determinar as medidas dos segmentos $x=PM$ e $y=DN$ em função dos segmentos $a$, $b$, $c$ e $d$.

Temos que a corda $AB=a+b$, onde $M$ é seu ponto médio. Assim:

$$
AM = \frac{a+b}{2}\\
\ \\
a + x = \frac{a+b}{2}\\
\ \\
2a + 2x = a + b\\
\ \\
2x = b - a\\
\ \\
x = \frac{b-a}{2}
$$

Analogamente, temos que a corda $CD=c+d$, onde $N$ é seu ponto médio. Assim:

$$
DN = \frac{c+d}{2}\
\ \\
y = \frac{c+d}{2}\\
$$

Vamos destacar o triângulo retângulo $OND$ da figura acima:

$$
r^2 = x^2 + y^2\\
\ \\
r^2 = \left(\frac{b-a}{2}\right)^2 + \left(\frac{c+d}{2}\right)^2\\
\ \\
r^2 = \frac{b^2-2ab+a^2}{4} + \frac{c^2+2cd + d^2}{4}\\
\ \\
4r^2 = b^2 + a^2 -2ab + c^2 + 2cd + d^2
$$

Mas, pelo teorema das cordas dado na relação $(3)$, temos que $a\cdot b = c \cdot d$. Assim:

$$
4r^2 = b^2 + a^2 -2ab + c^2 + 2ab + d^2
$$
O que nos leva ao teorema de Faure:
$$
4r^2 = a^2 + b^2 + c^2 + d^2
$$

Links para este artigo:

• http://bit.ly/Teorema-Faure
• https://www.obaricentrodamente.com/2019/12/o-teorema-de-faure.html

Veja mais:

• O teorema do ângulo inscrito
• O teorema de Pitágoras
• Os pontos de Brocard