O primeiro matemático a operar com números complexos, ao invés de simplesmente rejeitá-los, como acontecia até então, foi Girolamo Cardano (1501–1576).
Resolvendo o problema de dividir o número $10$ em duas partes cujo produto é $40$, provou que os números $5+\sqrt{-15}$ e $5-\sqrt{-15}$ são os fatores:
$$40 = (5+\sqrt{-15}) \times (5-\sqrt{-15})\\
\ \\
40 = 5\times 5 - 5\times \sqrt{-15} + 5\sqrt{-15} - \sqrt{-15}\times \sqrt{-15}\\
\ \\
40 = 25 + 15\\
\ \\
40 = 40
$$
Esses fatores são as raízes da equação $x^2-10x+40=0$. Utilizando a fórmula de Bháskara, obtemos:
$$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\ \\
x = \frac{10 \pm \sqrt{(-10)^2-4\cdot 1 \cdot 40}}{2\cdot 1}\\
\ \\
x = \frac{10 \pm \sqrt{100 - 160}}{2}\\
\ \\
x = \frac{10\pm \sqrt{-60}}{2}\\
\ \\
x = \frac{10 \pm 2\sqrt{-15}}{2}\\
\ \\
x_1 = 5 + \sqrt{-15}\\
\ \\
\text{e}\\
\ \\
x_2=5 - \sqrt{-15}
$$
Mas, ao aplicar a fórmula hoje conhecida por seu nome à equação $x^3-15x-4$, obteve:
$$x = \sqrt[\Large3]{2+\sqrt{-121}}+\sqrt[\Large 3]{2-\sqrt{-121}}
$$
No entanto, Cardano não soube como transformar a expressão acima em $4$, que sabia ser uma das raízes procuradas.
Quem tirou a matemática desse impasse foi o bolonhês Rafael Bombelli (1526–1572), notável diletante da matemática. Fazendo:
$$\sqrt[\Large 3]{2+\sqrt{-121}} = a+b\sqrt{-1}\\
\ \\
\text{e}\\
\ \\
\sqrt[\Large 3]{2-\sqrt{-121}} = a-b\sqrt{-1}
$$
obteve $a=2$, $b=1$ e por fim $x=4$.
Mas Bombelli foi além. Em seu livro publicado em 1572, intitulado Álgebra, aparece pela primeira vez uma teoria dos números complexos razoavelmente bem estruturada, inclusive com uma notação específica. O número $3i$, por exemplo, era representado por:
$$R\Big[0\ \text{m.}\ 9\Big]
$$
onde $R$ vem de "raiz" e $\text{m}$ vem de "menos", ou seja:
$$R\Big[0\ \text{m.}\ 9\Big] = \sqrt{0-9}
$$
Contudo, os números complexos seguiram mantendo uma aura de mistério até a virada do século $XVIII$ para o $XIX$, quando Caspar Wessel (1745–1818), Johann Carl Friedrich Gauss (1777–1855) e Jean-Robert Argand (1768–1822) descobriram de forma independente que esses números admitem uma representação geométrica.
Mas, enquanto Gauss imaginava essa representação por meio de um plano, Wessel e Argand usavam segmentos de reta orientados ou vetores para representá-los. Na verdade, Wessel e Argand, dois amadores da matemática, escreveram trabalhos específicos a respeito, e com enfoques muito parecidos, sendo Wessel quem primeiro publicou em 1799.
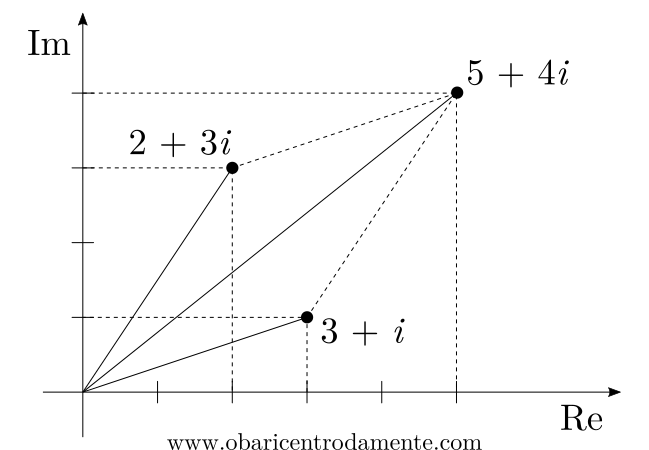
Todos, contudo, perceberam que, mais do que para representar pontos ou vetores, os números complexos podem ser utilizados para operar algebricamente com eles. Ou seja, os números complexos se constituem na álgebra dos vetores de um plano.
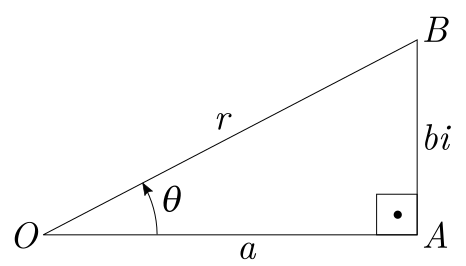
Modernamente um plano cartesiano usado para representar os números complexos costuma ser chamado de plano de Argand-Gauss. Em verdade essa representação se aproxima mais das contribuições de Argand o assunto. Este último, trabalhando com a ideia de rotação, considerava um número complexo $a+bi$ como soma vetorial $OB$ de $a$ e $bi$, conforme ilustra a imagem abaixo, ou, na forma trigonométrica como $r(\cos (\theta)+ i\ \text{sen}(\theta))$.
Algebricamente, porém, havia um ponto importante a elucidar: como entender uma soma $a+bi$, considerando que as parcelas $a$ e $bi$ são entes de espécie diferente? Quem tomo a si essa tarefa foi William Rowan Hamilton (1805-1865).
Hamilton nasceu em Dublin, Irlanda, e ficou órfão de pai e mãe ainda menino. Mas, mesmo antes do desfecho desses acontecimentos, sua educação já fora confiada a um tio que era linguista. Assim, sua rara precocidade intelectual foi canalizada inicialmente para o aprendizado de línguas: aos 5 anos de idade era fluente em grego, latim e hebraico; aos 8 em francês e italiano; aos 10 em árabe e sânscrito e aos 14 em persa. Por essa época, aproximadamente começa a se interessar por matemática e física. Pôs-se a ler grandes obras como os Principia de Isaac Newton e a Mecânica celeste de Laplace. Aos 18 anos publicou um trabalho corrigindo um erro no trabalho de Laplace. Em 1824 ingressou no Trinity College de Dublin, onde mais tarde, em 1827, tornou-se professor de astronomia mesmo ainda sem haver se graduado. Com isso, passou a ser, inclusive, astrônomo real da Irlanda.
Em um artigo de 1833 apresentado à Academia Irlandesa, Hamilton introduziu álgebra formal dos números complexos, que, segundo sua ideia básica, passavam a ser encarados como pares ordenados $(a,b)$ de números reais, com os quais se operava segundo as leis:
$$(a,b)+(c,d)=(a+c,b+d)\\
\ \\
(a,b)\cdot (c,d)=(ac-bd,ad+bc)
$$
Nessa ordem, um par $(a,0)$ equivale ao número real $a$. Em particular $(-1,0)=-1$. Assim, fazendo $i=(0,-1)$, obtém-se:
$$i^2 = (0,-1)\cdot (0,-1)\\
\ \\
i^2 = (-1,0)\\
\ \\
i^2 = -1
$$
E finalmente obtinha-se uma explicação lógica para o símbolo $\sqrt{-1}$.
Mas o que Hamilton tinha em vista quando colheu esses resultados era algo mais pretencioso: buscar uma estrutura algébrica que fosse para os vetores do espaço tridimensional o mesmo que a dos números complexos é para os vetores de um plano. Assim, como um número complexo tem a forma:
$$(a,b)=a+bi
$$
a expressão desses novos entes tridimensionais deveria ser:
$$(a,b,c) = a + bi + cj
$$
Durante mais de 10 anos Hamilton procurou inutilmente uma regra para definir a multiplicação que gozasse das propriedades algébricas esperadas, ou seja, as mesmas da multiplicação de pares ordenados (a adição não oferecia dificuldades).
Um dia, em 1843, ocorreu-lhe que seria preciso buscar quádruplos em vez de ternos e abandonar a comutatividade da multiplicação. Nasciam assim os quatérnios $a+bi+cj+dk$, em que:
$$i^2 = j^2 = k^2 = -1\\
\ \\
ij = k = -ji\\
\ \\
jk = i = -kj\\
\ \\
ki = j = -ik
$$
Hamilton depositava grande confiança na aplicabilidade dos quatérnions. Por essa razão investiu, daí em diante, grande parte de seu tempo para desenvolver a álgebra que criara. Se os resultados não foram os desejados, pelo menos romperam os grilhões da comutatividade na álgebra e, sem dúvida, foi um dos grandes avanços da matemática de todos os tempos.
Texto de:
Hygino H. Domingues
Referências:
- Fundamentos de Matemática Elementar V6 - Complexos, Polinômios e Equações - Gelson Iezzi
Links para este artigo:
- https://bit.ly/numeros-complexos-cardano-hamilton
- https://www.obaricentrodamente.com/2022/01/os-numeros-complexos-de-cardano-a-hamilton.html
Veja mais:
- Estudo sobre números complexos
- Introdução e influência dos quatérnios
- Uma demonstração de que i elevado a i é um número real
- Em uma divisão de números complexos, por que devemos multiplicar o divisor e o dividendo pelo conjugado do divisor?



Eu nunca tive a oportunidade de trabalhar esse assunto no Ensino Médio. A coordenação que escolhia qual turma eu ia ensinar. Geralmente pegava o 3º ano (que adorava por conta de Geometria Analítica).
ResponderExcluirMas, sempre quando dava aulas sobre conjuntos numéricos no fundamental e chegava em $\mathbb{R}$, eu falava que tinha mais conjuntos que seriam estudados no ensino médio. A curiosidade e a conversa durante a aula se estendia até falar sobre Complexos.
Daí falava em Geometria, 3D, falava dos filmes da Pixar, etc. Os alunos ficavam doidos! Aliás eu compartilhei sobre isso no blog. São esses:
Matemática: o verdadeiro segredo para a criação dos personagens da Pixar e Khan Academy lança o 'Pixar in a Box' e mostra a Matemática por trás de suas animações.
Obrigado por sempre citar meus posts.
Abraço meu amigo!
Uma pena você não ter podido ensinar o conjunto dos complexo, seriam boas aulas.
ExcluirCada vez que leio sobre a história da matemática me surpreendo com algo novo. Não sabia da participação de Hamilton na álgebra complexa.
Cito seus posts porque são bons e nossa parceria melhor aidna.
Uma abraço!