Veremos neste artigo como construir a fórmula para o cálculo da área de uma esfera. Para isso, utilizaremos o conceito de integral definida e a fórmula para calcular o comprimento de arco de uma curva.
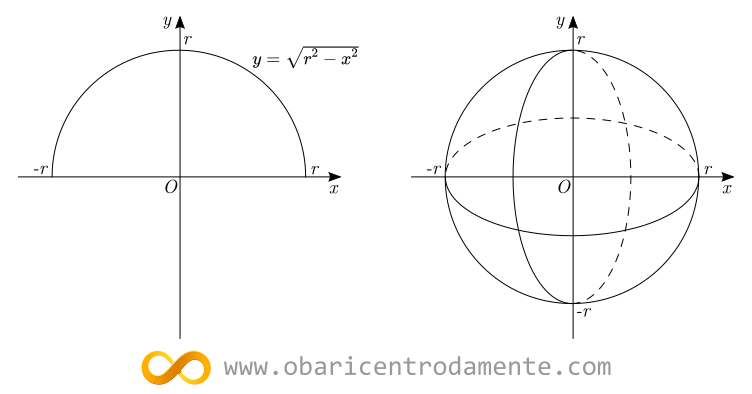
Para encontrarmos uma fórmula que expresse a área da superfície de uma esfera, podemos considerá-la como uma superfície de revolução, obtida ao girarmos a semicircunferência $y=\sqrt{r^2-x^2}$ em torno do eixo dos $x$:
Sendo assim, se tomarmos um segmento de comprimento infinitesimal $da$ sobre a curva $f(x)=\sqrt{r^2-x^2}$, quando esta for girada em torno do eixo do $x$, produzirá uma superfície infinitesimal de área $dA$ e se o ponto médio de $da$ estiver a uma distância $y$ do eixo dos $x$, teremos:
$$dA = 2\pi y\ da \tag{1}
$$
onde $dA$ é o elemento diferencial de área, $y$ é o raio da circunferência de comprimento $c=2\pi y$ e $da$ é o elemento diferencial de comprimento de arco.
O comprimento de um arco de curva pode ser calculado utilizando a fórmula abaixo, obtida através do Cálculo Diferencial e Integral:
$$da = \sqrt{1+\left(\frac{dy}{dx}\right)^2} \tag{2}
$$
Se você, leitor, quiser entender melhor como a fórmula $(2)$ foi obtida, leia o artigo Como calcular o comprimento de um arco de curva.
Assim, a relação $(1)$ se transforma em:
$$dA = 2\pi y \sqrt{1+\left(\frac{dy}{dx}\right)^2} \tag{3}
$$
Para encontrarmos a área total da superfície da esfera, devemos somar os infinitos elementos de área $dA$ com $y$ variando de $r$ a $-r$. Mas, podemos utilizar a simetria da esfera, uma vez que ela se encontra centrada na origem. Assim, utilizamos os limites de integração de $0$ a $r$:
$$A = 2 \int _0^r 2\pi y \sqrt{1+\left(\frac{dy}{dx}\right)^2} dx \tag{4}
$$
Mas como $y=\sqrt{r^2-x^2}$, fazemos:
$$A = 2 \int _0^r 2\pi \sqrt{r^2-x^2} \sqrt{1+\left(\frac{dy}{dx}\right)^2} dx \tag{5}
$$
Ainda falta calcularmos a derivada de $f(x)$ antes de realizarmos a integração
$$f(x) = \sqrt{r^2-x^2}\\
\ \\
f(x) = \big(r^2-x^2\big)^{1/2}\\
\ \\
f^\prime(x) = \frac{1}{2} \big(r^2-x^2\big)^{-1/2}\cdot (-2x)\\
\ \\
f^\prime (x)= \frac{-x}{\sqrt{r^2-x^2}}
$$
Substituindo na relação $(5)$, obtemos:
$$A = 2 \int _0^r 2\pi \sqrt{r^2-x^2} \sqrt{1+\left( \frac{-x}{\sqrt{r^2-x^2}} \right)^2} dx\\
\ \\
A = 4\pi \int _0^r \sqrt{r^2-x^2} \sqrt{1+\frac{x^2}{r^2-x^2}} dx\\
\ \\
A = 4\pi \int _0^r \sqrt{r^2-x^2} \sqrt{\frac{r^2-x^2+x^2}{r^2-x^2}} dx\\
\ \\
A = 4\pi \int _0^r \sqrt{r^2-x^2} \sqrt{\frac{r^2}{r^2-x^2}} dx\\
\ \\
A = 4\pi \int _0^r \sqrt{\frac{r^2(r^2-x^2)}{r^2-x^2}} dx\\
\ \\
A = 4\pi \int _0^r r \ dx\\
\ \\
A = 4\pi \big[ r \cdot x \big]_0^r\\
\ \\
A = 4\pi \big[ r\cdot r - r \cdot 0 \big]\\
\ \\
A = 4\pi r^2
$$
Referências:
- Cálculo com Geometria Analítica V1 - Simmons
- Cálculo 1 - Munem & Foulis
Links para este artigo:
- https://bit.ly/area-esfera-integral
- https://www.obaricentrodamente.com/2022/06/como-encontrar-a-formula-da-area-da-esfera-atraves-de-integral.html




Postar um comentário