Este é o segundo artigo sobre como encontrar a área de uma região quando dois arcos de circunferência são descritos internamente a um quadrado. Para ler a parte 1 dessa série de artigos, acesse o link abaixo:
Seja um quadrado de lado $r$ e sejam dois arcos e circunferência de raios iguais a $r$, cujos centros encontram-se em dois vértices opostos do quadrado. Vamos calcular a área hachurada correspondente à intersecção desses dois arcos.
Um método de resolução é traçar a uma diagonal dividindo a área hachurada em duas partes simétricas, calcular a área de um segmento circular e multiplicar por dois.
Iniciamos nomeando cada vértice e traçando a diagonal $\overline{AC}$, gerando dois segmentos circulares referentes aos arcos $ABC$ e $ADC$.
A área de um segmento circular é dada por:
$$A_S = \frac{r^2}{2} \big(\theta - \text{sen}(\theta)\big)
$$
onde $\theta$ é o ângulo central em radianos e $r$ é o raio da circunferência.
Isolando cada arco de circunferência, termos algo parecido com o esquema abaixo.
Como o ângulo central é de $90°$, logo:
$$A_S = \frac{r^2}{2} \big(\theta - \text{sen}(\theta)\big)\\
\ \\
A_S = \frac{r^2}{2} \left(\frac{\pi}{2} - \text{sen}\left(\frac{\pi}{2}\right)\right)\\
\ \\
A_S = \frac{r^2}{2} \left( \frac{\pi}{2} - 1\right)
$$
Por simetria, a área hachurada será duas vezes a área encontrada acima. Assim:
$$A_H = 2 \cdot \frac{r^2}{2} \left( \frac{\pi}{2} - 1\right)
$$
Obtendo finalmente a fórmula para a área hachurada:
$$A_H = r^2 \left( \frac{\pi}{2} - 1\right) \tag{1}
$$
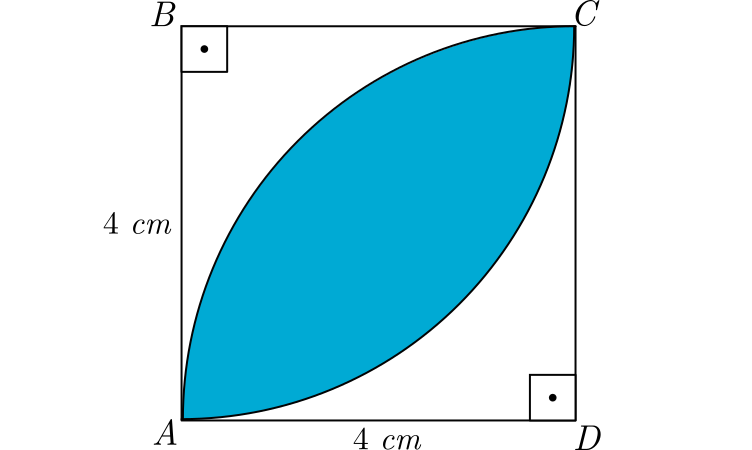
Exemplo 1:
Calcular a área hachurada da figura abaixo sabendo que o quadrado possui $4\ cm$ de lado.
Substituímos o lado do quadrado que mede $r=4\ m$ na fórmula encontrada em $(1)$:
$$A_H = r^2 \left( \frac{\pi}{2} - 1\right) \\
\ \\
A_H = 4^2 \left( \frac{\pi}{2} - 1\right)\\
\ \\
A_H = 16 \left( \frac{\pi}{2} - 1\right)\\
\ \\
A_H \approx 9,1327 \ cm
$$





continuaaa,vou maratona todas suas publicações aqui..vlw dmais mestre
ResponderExcluirObrigado, meu amigo, pelo prestígio! Abraço!
ExcluirExcelente!!!
ResponderExcluir