- Como calcular a área envolvendo um quadrado e dois arcos de circunferência - Parte 1
- Como calcular a área envolvendo um quadrado e dois arcos de circunferência - Parte 2
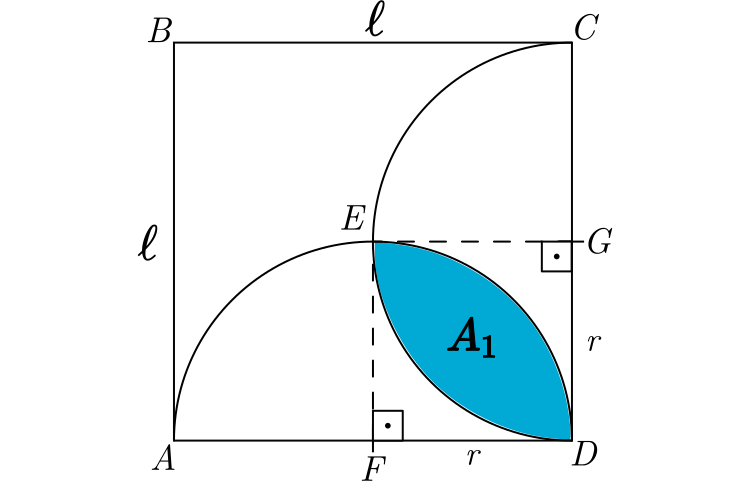
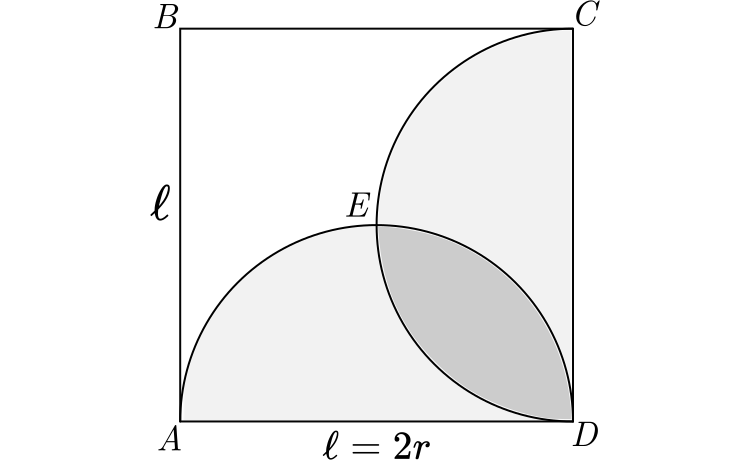
Seja um quadrado de lado $\ell$ e sejam dois arcos e circunferência de raios iguais a $r=\cfrac{\ell}{2}$, cujos centros encontram-se nos pontos médios de dois lados adjacentes do quadrado. Vamos calcular a área hachurada $A_1$ correspondente à intersecção desses dois arcos e a área $A_2$, que é a área limitada pelo quadrado e os dois semicírculos.
Cálculo da área $A_1$:
A área $A_1$ já vimos como calcular no segundo artigo desta série de posts e é dada por:
$$A_1 = r^2 \left(\frac{\pi}{2}-1\right)
$$
onde $r$ é o raio da circunferência e o lado do quadrado $DFEG$.
Cálculo da área $A_2$:
A área $A_2$ é dada pela área do quadrado $ABCD$, subtraindo a área da figura formada pelos semicírculos $AECD$.
A área da figura $AECD$ é a soma das áreas dos dois semicírculos $AED$ e $DEC$ (igual à $\pi r^2$), subtraindo a área $A_1$, pois está sendo somada duas vezes. Assim:
$$A_{AECD} = \pi r^2 - r^2 \left( \frac{\pi}{2}-1\right)
$$
E para calcular a área $A_2$, fazemos:
$$A_2 = A_Q - A_{AECD}\\
\ \\
A_2 = \ell^2 - \left[ \pi r^2 - r^2 \left( \frac{\pi}{2}-1 \right)\right]\\
\ \\
A_2 = 4r^2 - \pi r^2 + \frac{\pi r^2}{2} - r^2\\
\ \\
A_2 = 3r^2 - \frac{\pi r^2}{2}\\
\ \\
A_2 = r^2 \left( 3 - \frac{\pi}{2}\right)
$$
Exemplo 1:
Calcular as áreas hachuradas $A_1$ e $A_2$ da figura abaixo sabendo que o quadrado possui $4\ cm$ de lado.
A área do quadrado é dada por:
$$A_Q = 4^2 = 16\ cm^2
$$
Como o lado do quadrado mede $\ell = 4\ cm$, o raio dos semicírculos medem $r=2\ cm$. Assim, a área $A_1$ será dada por:
$$A_1 = r^2 \left(\frac{\pi}{2}-1\right)\\
\ \\
A_1 = 4\left(\frac{\pi}{2}-1\right)\\
\ \\
A_1 = 2\pi - 4 \\
\ \\
A_1 \approx 2,283\ cm^2
$$
A área $A_2$ é dada por:
$$A_2 = r^2 \left( 3 - \frac{\pi}{2} \right)\\
\ \\
A_2 = 4 \left( 3 - \frac{\pi}{2} \right)\\
\ \\
A_2 \approx 5,7168\ cm^2
$$





Muito interessante! Obrigado por postar
ResponderExcluirAgradeço por ler e comentar o artigo!
Excluir