Arquimedes de Siracusa (287 a.C. - 212 a.C.), sem dúvida alguma, foi o maior matemático da antiguidade e um dos maiores de todos os tempos. Seus trabalhos envolviam matemática, física, astronomia e engenharia.
Arquimedes se dedicou, em grande parte, às propriedades geométricas do círculo e uma de suas conclusões foi que o valor de $\pi$ se encontrava entre $233/71$ e $22/7$ e para isso utilizou o método de inscrever e circunscrever polígonos regulares a um círculo.
Arquimedes tinha conhecimento de que uma circunferência é proporcional a seu diâmetro e uma forma de expressar esse teorema é "As circunferências estão entre si como seus diâmetros".
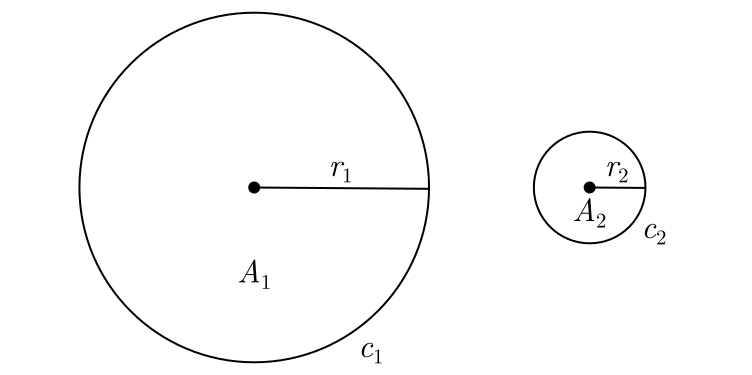
Vamos considerar dois círculos de raios $r_1$ e $r_2$, cujos comprimentos de suas circunferências medem $c_1$ e $c_2$, respectivamente. Consequentemente, seus diâmetros serão $d_1=2r_1$ e $d_2=2r_2$. O teorema da proporcionalidade entre os comprimentos e os diâmetros pode ser expresso como:
$$\frac{c_1}{c_2} = \frac{d_1}{d_2} =\frac{2r_1}{2r_2} = \frac{r_1}{r_2} \tag{1}
$$
O símbolo $\pi$ fora usado anteriormente pelos matemáticos ingleses Willian Oughtred, Isaac Barrow e David Gregory para designar a circunferência de um círculo. O primeiro a usar esse símbolo para a razão entre a circunferência e o diâmetro foi o escritor inglês William Jones, numa publicação de 1706. Porém, o símbolo só encontrou aceitação geral depois que Leonhard Euler (1707-1783) o adotou em 1737.
A definição de $\pi$ pode ser expressa através de uma fórmula que relaciona o comprimento da circunferência $(c)$, seu diâmetro $(d)$ e seu raio $(r)$, sendo válida para qualquer círculo:
$$\pi = \frac{c}{d} = \frac{c}{2r} \tag{2}
$$
A partir desta definição, o comprimento da circunferência de um círculo qualquer pode ser expresso como:
$$c = 2\pi r \tag{3}
$$
Em 1761, Johann Heinrich Lambert provou que $\pi$ é irracional. Isso quer dizer que não pode ser expresso como uma razão entre dois números inteiros do tipo $\cfrac{a}{b}$, sendo $b \neq 0$.
Arquimedes não mencionou em seus trabalho algo relacionado à irracionalidade de $\pi$, mas obteve uma excelente aproximação mencionada em seu trabalho A Medida de um Círculo. Infelizmente esse tratado não chegou até nós em sua forma original e pode tratar-se apenas de um fragmento de uma discussão mais ampla.
Neste trabalho, Arquimedes encontrou limites superiores e inferiores para $\pi$ inscrevendo e circunscrevendo em um círculo polígonos regulares de $n$ lados. Uma vez que é relativamente mais simples calcular os perímetros de polígonos regulares, facilmente se obtém limites para $\pi$. A imagem abaixo mostra parte do processo:
Podemos ver que quando o número $n$ de lados dos polígonos aumenta, seus perímetros ficam cada vez mais próximos da circunferência e se tomarmos polígonos com um número muito grande de lados, obteremos valores cada vez mais próximos de $\pi$.
Quando Arquimedes utilizou nesse processo polígonos de 96 lados, chegou à conclusão de que o valor da razão entre a circunferência e seu diâmetro era maior do que $3\cfrac{10}{71}$ e menor do que $3\cfrac{1}{7}$, correto até a segunda casa decimal:
$$3\frac{10}{71} < \frac{c}{d} < 3\frac{1}{7} \tag{4}
$$
Combinando a relação $(2)$ com a $(4)$, obtemos os limites de $\pi$ encontrados por Arquimedes:
$$3,1408 < \pi < 3,1429 \tag{5}
$$
Esses notáveis valores obtidos por Arquimedes são os mais famosos da antiguidade grega.
Desde os matemáticos Eudoxo de Cnido (408 a.C. - 355 a.C.) e Euclides de Alexandria (325 a.C. - 265 a.C.), era conhecido que a área de qualquer círculo é proporcional ao quadrado de seu diâmetro. A proposição 2 do livro XII dos Elementos de Euclides diz que:
"Os círculos estão entre si como os quadrados em seus diâmetros."
Considere os círculos de raios $r_1$ e $r_2$, cujos diâmetros são $d_1$ e $d_2$ e cujas áreas são $A_1$ e $A_2$, respectivamente:
Podemos expressar a proposição de Euclides como:
$$\frac{A_1}{A_2} = \left( \frac{d_1}{d_2}\right)^2 = \left( \frac{r_1}{r_2}\right)^2 \tag{6}
$$
Arquimedes foi além de Eudoxo e Euclides. Em A medida de um círculo, provou que:
Proposição 1: A área de qualquer círculo é igual a um triângulo retângulo no qual um dos catetos possui medida igual ao raio e o outro cateto igual à circunferência.
Seja $A$ a área de um círculo de raio $r$ e comprimento da circunferência $c$. Seja $A_T$ a área de um triângulo no qual seus catetos medem $c$ e $r$. O resultado obtido por Arquimedes pode ser expresso pela fórmula:
$$A = A_T = \cfrac{c \cdot r}{2} \tag{7}
$$
Se combinarmos as relações $(2)$ , $(3)$ e $(7)$ obtemos:
$$A=A_T=\frac{c \cdot r}{2} = \frac{2\pi r \cdot r}{2}=\pi r^2 \tag{8}
$$
Que é a fórmula moderna para a área de um círculo.
Referências:
- O Método Ilustrado de Arquimedes - André K. T. Assis
- Introdução à História da Matemática - Howard Eves







Parabéns pela escrita desse ótimo texto, Kleber.
ResponderExcluirEu que agradeço, Valdo, por dedicar seu tempo na leitura e comentar! Um abraço!
Excluir