Ao início do século XVII, os métodos deixados pelos gregos para cálculos de áreas e volumes, apesar de sua beleza e rigor, mostravam-se cada vez menos adequados a um mundo em franco progresso científico, pois faltavam a eles operacionalidade e algoritmos para implementá-los. E como não havia ainda condições matemáticas de obter esses requisitos, os métodos então surgidos eram sempre passíveis de críticas — como o mais famoso deles, a geometria dos indivisíveis de Cavalieri (1598-1647), que se tornou um fator no desenvolvimento do Cálculo Integral. Em sua obra Geometria Indivisibilibus, de 1635 e a subsequente Exercitationes Geometricæ sex, de 1647, foram as tentativas mais sérias de transformar o que era uma coleção de práticas matemáticas se muito rigor em um "método" sistemático. Todas as discussões subsequentes sobre indivisíveis no século XVII referem-se repetidamente ao seu trabalho.
Bonaventura Francesco Cavalieri nasceu em Milão, Itália, no ano de 1598 e morreu em 30 de novembro de 1647 em Bolonha, Itália.
Cavalieri foi um dos matemáticos mais influentes de sua época. De família nobre, Cavalieri seguiu paralelamente a carreira religiosa e a atividade científica. Discípulo de Galileu Galilei (1564-1642), por indicação deste ocupou desde 1629 a cátedra de Matemática da Universidade de Bolonha (em princípio, seria por um período experimental de 3 anos, mas que acabou sendo prorrogado), ao mesmo tempo que era o superior do monastério de São Jerônimo. Publicou onze livros durante seus dezoito anos em Bolonha. Cavalieri foi também astrônomo, mas, se ainda é lembrado, isso se deve em grande parte ao método dos indivisíveis que desenvolveu a partir de 1626.
Mas o que há no método dos indivisíveis que o torna atraente para os amantes da matemática?
Cavalieri não definia, em suas obras sobre o assunto, o que vinham a ser os indivisíveis. Segundo ele, porém, uma figura plana seria formada por uma infinidade de cordas paralelas entre si e uma figura sólida por uma infinidade de seções planas paralelas entre si — a essas cordas e a essas seções chamava de indivisíveis. Num de seus livros “explicava” que um sólido é formado de indivisíveis, assim como um livro é composto de páginas. Do ponto de vista lógico, essas ideias envolviam uma dificuldade insuperável. Como uma figura de extensão finita poderia ser formada de uma infinidade de indivisíveis, tanto mais que estes não possuem espessura?
Em 1586, Simon Stevin (1548-1620), engenheiro, físico e matemático, em sua obra O Princípio da Estática, demonstrava que o centro de gravidade de um triângulo esta sobre sua mediana. Para isso, utilizou-se de infinitos paralelogramos de altura infinitesimal inscritos em um triângulo, que se confundiam com um segmento de reta. Logo, o centro de gravidade desta "reta" seria seu ponto médio. Aplicando o método referente aos três lados do triângulo, obtinha-se que o baricentro do triângulo recai no encontro das medianas.
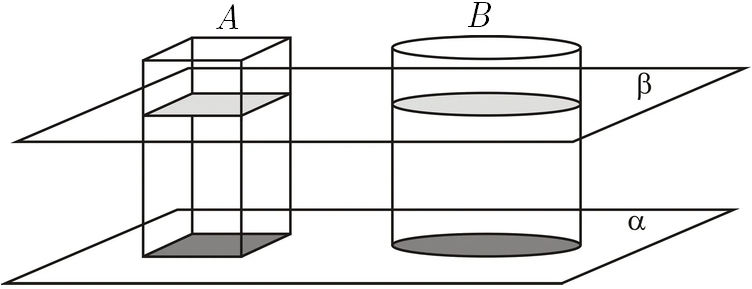
O princípio de Cavalieri, ainda bastante usado no ensino de geometria métrica no espaço, facilita bastante a aceitação da ideia de indivisível:
“Sejam dois sólidos A e B. Se todos os planos numa certa direção, ao interceptarem A e B, determinam seções (indivisíveis) de áreas iguais, então A e B têm mesmo volume”:
De alcance maior foram certos teoremas estabelecidos por Cavalieri, como o que aparece na proposição 19 do livro Exercitationes Geometricæ sex, de 1647, que diz que:
"Se em um paralelogramo uma diagonal é traçada, então o paralelogramo é o dobro de qualquer um dos triângulos construídos por esta diagonal".
Cavalieri dividiu um dos triângulos em um número infinito de segmentos paralelos às bases $CD$ e $AF$ (este são os "indivisíveis") e relacionou com os indivisíveis do próprio paralelogramo. Ele, então, argumentou que, como cada um dos segmentos de um triângulo tinha seu equivalente no outro (por exemplo $HE=BI$) então, "todos os segmentos" de um triângulo eram iguais a "todos os segmentos" do outro, concluindo que as áreas dos dois triângulos eram iguais e que, portanto, o paralelogramo era o dobro de qualquer um deles.
Se $a$ indica genericamente os indivisíveis do paralelogramo e $x$ indica os indivisíveis de um dos triângulos, Cavalieri provou que:
$$\begin{cases}
\sum a = 2\sum x\\
\ \\
\sum a^2 = 3\sum x^2\\
\ \\
\cdots
\end{cases}
\tag{1}
$$
onde os somatórios não têm o sentido atual, mas correspondem à ideia de "integrar" os indivisíveis para formar uma figura, ou seja, os segmentos de comprimento $x$ que vão de $C$ até $AF$, quando somados, representam a metade do paralelogramo, que é formado pela soma dos segmentos de comprimento $a$, que vão de $CD$ até $AF$.
Se o paralelogramo é um retângulo de altura $b$, sua área $\sum a$ é igual ao produto de um divisível pelo “número” $b$ de indivisíveis, isto é, $\sum a = ab$. Usando então a primeira das relações de $(1)$, obtém-se a área do triângulo:
$$
\sum x = \frac{1}{2} \sum a = \frac{1}{2} ab
$$
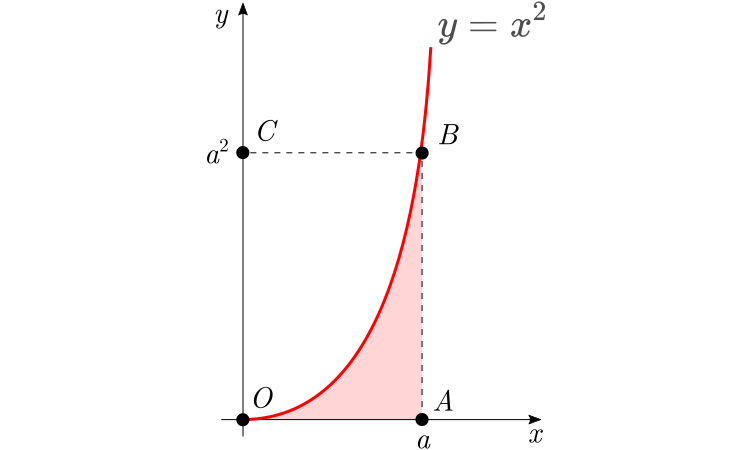
A segunda das relações de $(1)$ permite calcular a área compreendida entre as curvas $y=x^2$ e o eixo $x$, de $O$ até $a$, conforme figura abaixo:
Segundo as ideias de Cavalieri, essa área vale $\sum x^2$, pois cada um de seus indivisíveis (ordenadas) vale $x^2$. Mas, pela relação citada:
$$
\sum x^2 = \frac{1}{3} \sum a^2
$$
onde $\sum a^2$ é a área do retângulo $OABC$.
Mas essa área é dada também por $a \cdot a^2 = a^3$ (base vezes altura). Logo, a área sombreada é $\cfrac{a^3}{3}$, resultado correto.
Foram tantas as críticas que Cavalieri recebeu pelo seu método, embora este funcionasse (como no exemplo anterior), que certa vez disse: "O rigor é algo que diz respeito à filosofia, e não à matemática".
Referências:
- Fundamentos de Matemática Elementar V10 - Geometria Espacial - Osvaldo Dolce & Nicolau Pompeo
- Introdução à História da Matemática - Howard Eves
- From Voyagers History of Mathematics - Amir Alexander
- Exercitationes Geometricæ Sex - Bonaventura Cavalieri
Links para este artigo:
- https://bit.ly/indivisiveis-cavalieri
- https://www.obaricentrodamente.com/2022/09/cavalieri-e-o-metodo-dos-indivisiveis.html




Postar um comentário