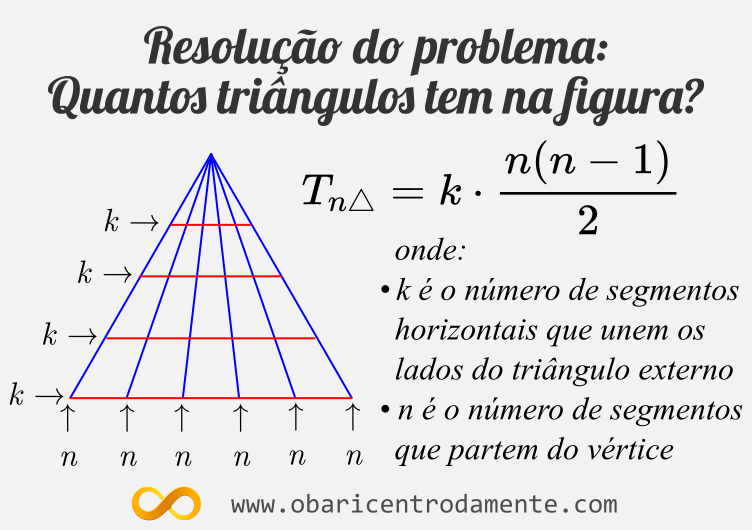
Um dos problemas que tomam o tempo de muitas pessoas e geram muitas discussões nas redes sociais é o de descobrir quantos triângulos tem em uma determinada figura, que contém um triângulo com vários segmentos partindo do vértice e vários segmentos horizontais, como na figura acima.
Quando o número de segmentos é pequeno, podemos apenas contar manualmente os triângulos formados. Mas quando o número de segmentos cresce, fica cada vez mais trabalhoso esse processo, o que pode levar a erros de contagem. Fora o tempo gasto.
Mas existe uma fórmula que pode ser aplicada e, assim, resolver o problemas em segundos.
O problema
Para este problema, existe uma variação infinita dependendo de quantos segmentos partem do vértice do triângulo dado e de quantos segmentos horizontais paralelos à base a figura possui. Sendo assim, podemos dividir a formação da imagem em duas partes:
1) Dado um triângulo, este possui um número $k \geq 1$, para $k \in \mathbb{N}$, de segmentos opostos ao vértice $V$, que formam um número $k$ de triângulos:
Imagem 1
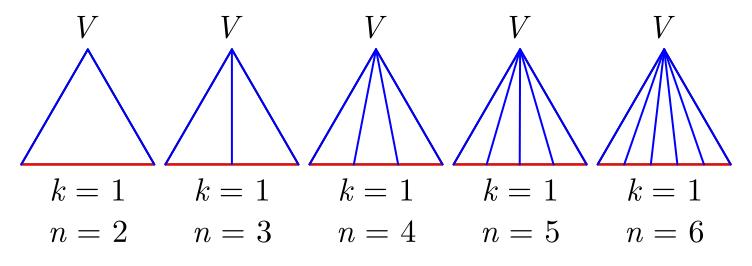
2) Dado um triângulo, este possui um número $n \geq 2$, para $n \in \mathbb{N}$, de segmentos que partem do vértice $V$ e seguem até à base do triângulo dado, formando um número $t$ de triângulos:
Imagem 2
O número $t$ de triângulos formados não cresce linearmente conforme o número $n$ de segmentos que partem do vértice cresce. Sendo assim, parte deste problema é determinar quantos triângulos são formados quando temos um número $n$ de segmentos.
A partir da imagem acima, podemos contar os triângulos formados e criar uma tabela de modo empírico:
Tabela 1
Lei de formação
Analisando a tabela acima, podemos observar alguns padrões na formação do problema:
a) Dados $n$ segmentos, o número total de triângulos $t$ é o produto de $n$ por $n-1$ segmentos, dividido por $2$:
$$t_n = \frac{n (n-1)}{2} \tag{1}
$$
Se aplicarmos esta fórmula observando os triângulos da imagem 2, podemos verificar que os dados da tabela 1 são verdadeiros. Mas, a fórmula é válida para qualquer quantidade de segmentos que partem do vértice $V$?
Demonstração
Para que possamos validar a fórmula $(1)$ temos que demonstrá-la, provando que se a fórmula é válida para um número $n$ de segmentos, também será válida para um número $n+1$ de segmentos.
Podemos fazer isso através do princípio da indução matemática, que é uma ferramenta muito útil na demonstração de proposições sobre o conjunto dos números naturais.
Seja $n_0$ um número inteiro e positivo. Suponhamos que para cada $n \geq n_0$ seja dada uma proposição $P(n)$. Queremos verificar as propriedades:
$i)$ $P(n_0)$ é verdadeira;
$ii)$ Se $P(n)$ é verdadeira, então $P(n+1)$ também é verdadeira para todo $n \geq n_0$
Então, $P(n)$ é verdadeira para qualquer $n \geq n_0$.
Por hipótese, temos que:
$$t_n = \frac{n(n-1)}{2} \tag{2}
$$
É fácil ver que, para $n=2$, a fórmula acima é verdadeira, pois dois segmentos que partem de um vértice até à base forma apenas um triângulo, o que verifica a propriedade $i)$:
Imagem 3
Se assumirmos que $P(n)$ é verdadeira, podemos mostrar que a fórmula também é válida para $n+1$ segmentos que partem de um vértice:
$$t_{n+1} = \frac{(n+1)(n)}{2} \tag{3}
$$
A tabela 1 foi criada por observação dos padrões de formação. Podemos ver que $t_{n+1}$ é formado pela soma de $t_n + n$. Assim:
$$t_{n+1} = t_n + n \tag{4}
$$
Substituindo a relação $(2)$ em $(4)$, obtemos:
$$t_{n+1} = \frac{n(n-1)}{2} + n\\
\ \\
t_{n+1} = \frac{n^2-n+2n}{2}\\
\ \\
t_{n+1} = \frac{n^2+n}{2}\\
$$
Fatorando $n$, obtemos:
$$t_{n+1} = \frac{n(n+1)}{2} \tag{5}
$$
Que é exatamente o que queríamos demonstrar.
Em busca de uma fórmula geral
Para um triângulo padrão, que possua apenas um segmento horizontal que une os lados do triângulo externo $(k=1)$, o padrão $\displaystyle t_n=\frac{n(n-1)}{2}$ aparece apenas uma vez:
Imagem 4
Se tivermos dois segmentos horizontais unindo os lados do triângulo externo $(k=2)$, o padrão $t_n$ aparecerá duas vezes:
Imagem 5
O número de vezes em que o padrão $t_n$ aparece é igual ao número de segmentos horizontais $(k)$ que a imagem contiver.
Sendo assim, o número total $T$ de triângulos formados por $n$ segmentos que partem do vértice $V$ à base do triângulo dado, e que possua um número $k$ de segmentos horizontais, é dado pela fórmula:
$$T_{n \triangle} = k \cdot \frac{n(n-1)}{2} \tag{6}
$$
Exemplo
A partir da fórmula $(6)$, podemos criar uma tabela contendo alguns triângulos, variando o número $k$ de segmentos horizontais e o número $n$ de segmentos que partem do vértice, e fazer algumas combinações:
Imagem 6
Sequência
A partir da fórmula $(6)$, podemos criar uma sequência numérica infinita com as quantidades de triângulos formados. Abaixo seguem os 100 primeiros números da sequência, considerando $k=1$ e $n \geq 2$ :
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431, 1485, 1540, 1596, 1653, 1711, 1770, 1830, 1891, 1953, 2016, 2080, 2145, 2211, 2278, 2346, 2415, 2485, 2556, 2628, 2701, 2775, 2850, 2926, 3003, 3081, 3160, 3240, 3321, 3403, 3486, 3570, 3655, 3741, 3828, 3916, 4005, 4095, 4186, 4278, 4371, 4465, 4560, 4656, 4753, 4851, 4950, 5050
Graficamente, podemos ver a evolução da quantidade de triângulos $T$ em relação ao número de segmentos $n$ que partem do vértice. O gráfico abaixo mostra uma curva para $n$ variando de $2$ a $1000$ e $k=1$:
Gráfico 1
Calculadora
Você pode utilizar a calculadora abaixo e inserir valores $k$ e $n$ para calcular quantos triângulos $T$ serão formados.
Calculadora de Triângulos
Desenvolvido por O Baricentro da Mente


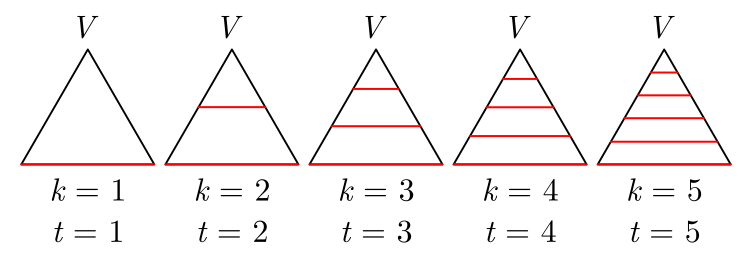






Excelente demonstração! Também é possível chegar a fórmula de T observando que quando K=1, a quantidade de triângulos
ResponderExcluirrepresenta uma progressão aritmética de segunda ordem.
Olá amigo! Não tinha visto por este lado. Vou tentar fazer aqui. Um abraço!
Excluir