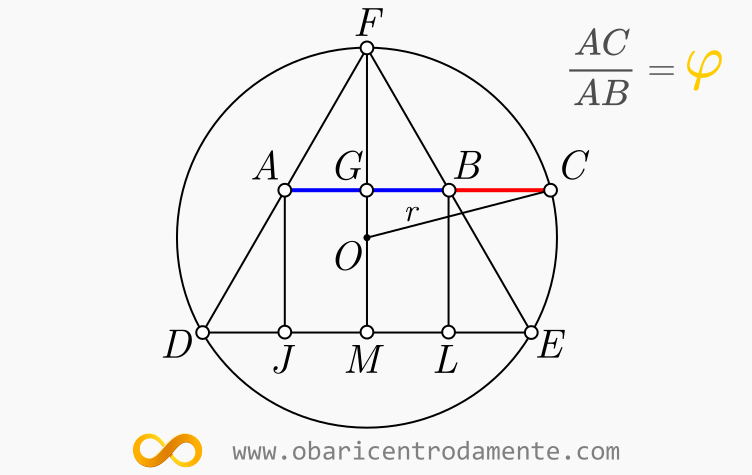
Esta construção foi desenvolvida por George Odom, publicada no American Mathematics Monthy, em 1983 e se dá com a circunferência circunscrita a um triângulo equilátero. Tomando os pontos médios de dois lados do triângulo, unimos esses pontos por um segmento de reta prolongando-o até a intersecção com a circunferência. A razão entre os segmentos $AC$ e $AB$ é PHI.
Sendo a os lados do triângulo equilátero inscrito à circunferência, temos que encontrar as medidas dos segmentos $AC$ e $AB$.
Considerando a figura abaixo, notem que, se $DF = a$, logo:
$$AF = \frac{a}{2} = AB \tag{1}
$$
Vamos determinar primeiramente a medida da altura $MF$ do triângulo:
$$DF^2 = MF^2 + DM^2\\
\ \\
a^2 = MF^2 + \frac{a^2}{4}\\
\ \\
MF^2 = a^2-\frac{a^2}{4}\\
\ \\
MF^2 = \frac{2a^2}{3}
$$
Extraindo a raiz de ambos os lados da igualdade, obtemos:
$$MF = \frac{a\sqrt{3}}{2} \tag{2}
$$
Como $DE=DJ+JL+LE=a$ e $\displaystyle JL=AB=\frac{a}{2}$, logo, o segmento $DJ$ é igual a:
$$DJ = \frac{a}{4} \tag{3}
$$
Vamos determinar a medida de $AJ$:
$$AD^2 = DJ^2 + AJ^2\\
\ \\
\frac{a^2}{4} = \frac{a^2}{16} + AJ^2\\
\ \\
AJ^2 = \frac{a^2}{4} - \frac{a^2}{16}\\
\ \\
AJ^2 = \frac{3a^2}{16}
$$
Extraindo a raiz de ambos os lados da igualdade, obtemos:
$$AJ = \frac{a\sqrt{3}}{4} \tag{4}
$$
Analisando a figura 2, vemos que:
\begin{cases}\displaystyle OM = \frac{1}{3} MF\\
\displaystyle AJ = OG + \frac{1}{3}MF
\end{cases}
Da segunda equação, temos:
$$OG = AJ - \frac{1}{3}MF\\
\ \\
OG = \frac{a\sqrt{3}}{4} - \frac{a\sqrt{3}}{6}\\
$$
Obtendo:
$$OG = \frac{a\sqrt{3}}{12} \tag{5}
$$
Podemos aplicar o teorema pitagórico no triângulo retângulo $OGC$, onde $r$ é o raio da circunferência que equivale a $2/3$ de sua altura:
$$r = \frac{2}{3}MF\\
\ \\
r = \frac{a\sqrt{3}}{3} \tag{6}
$$
Temos que:
$$r^2 = OG^2 + GC^2\\
\ \\
\left(\frac{3a^2}{3}\right)^2 = \left(\frac{a\sqrt{3}}{12}\right)^2 + GC^2\\
\ \\
\frac{3a^2}{9} = \frac{3a^2}{144} + GC^2
$$
O segmento $AC=AG+GC$, assim $\displaystyle AG=\frac{a}{4}$. Logo:
$$AC = \frac{1}{4} + \frac{a\sqrt{5}}{4}\\
\ \\
AC = \frac{a\big( 1 + \sqrt{5} \big)}{4} \tag{8}
$$
A razão áurea nesta construção é dada por $\displaystyle \frac{AC}{AB} = \varphi$:
$$\varphi = \frac{\displaystyle \frac{a\big(1+\sqrt{5}\big)}{4}}{\displaystyle \frac{a}{2}}\\
\ \\
\varphi = \frac{a\big(1+\sqrt{5}\big)}{4}\cdot \frac{2}{a}\\
\ \\
\varphi = \frac{1+\sqrt{5}}{2}\\
\ \\
\varphi = 1,618\cdots
$$
Notem que esta construção independe do raio da circunferência.



De fato, assim como as outras duas esta é uma bela construção. Boa série de postagens!!
ResponderExcluirOlá, Kleber!
ResponderExcluirDessa vez não foi preciso lançar mão de três circunferências para se encontrar o PHI, coisa que você tinha avisado. Agora, na minha opinião, das três construções, essa aqui é a mais prática!
Ótima postagem e como das vezes anteriores, receba os meus parabéns!
Um abraço!!!!!
Essa construção acho que é a mais interessante das 3, pois a razão áurea independe do tamanho do raio. Isso a torna "universal", de certa forma.
ResponderExcluirAbraços, amigos!